Insieme delle parti
Cos'è l'insieme delle parti?
L'insieme delle parti P(A) è l'insieme dei sottoinsiemi propri e impropri di A. $$ P(A) = \{ S | S ⊆ A \} $$ E' anche detto insieme potenza.
Ogni sottoinsieme S={s1,...} è una parte o componente dell'insieme A.
$$ S ⊆ A $$
Ogni sottoinsieme S è anche un elemento dell'insieme delle parti P(A).
$$ S \in P(A) $$
Nota. In questo caso il sottoinsieme è un elemento perché appartiene all'insieme P(A). Per questa ragione uso la relazione di appartenenza S∈P(A). In questo caso, S non è incluso nell'insieme P(A). S è soltanto incluso nell'insieme A ossia S⊆A.
Un esempio pratico di insieme delle parti
L'insieme A è composto dagli elementi a e b.
$$ A = \{ a,b \} $$
Gli elementi a,b appartengono all'insieme A
$$ a,b \in A $$
Ecco il diagramma di Venn dell'insieme.
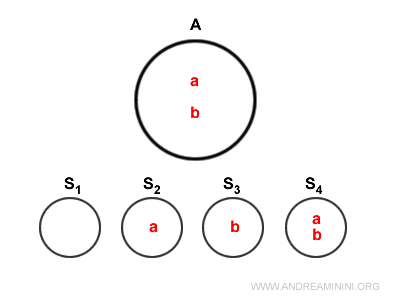
All'insieme delle parti P(S) appartengono tutti i sottoinsiemi di A.
$$ \{ \} \\ \{ a \} \\ \{ b \} \\ \{ a,b \} $$
Quindi l'insieme delle parti è composto dai seguenti elementi
$$ P(A) = \{ \{ \} , \{ a \} , \{ b \} , \{ a,b \} \} $$
ossia
$$ P(A) = \{ Ø , \{ a \} , \{ b \} , A \} $$
I sottoinsiemi {a} e {b} sono i sottoinsiemi propri di A.
I sottoinsiemi Ø e A sono i sottoinsiemi impropri di A.
Nota. Essendo degli elementi di P(A) posso anche scrivere $$ Ø , \{ a \} , \{ b \} , A \in P(A) $$
Ecco il diagramma di Venn dell'insieme delle parti P(A).
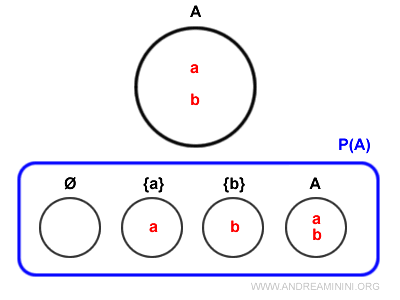
Come si può notare anche l'insieme A è un elemento dell'insieme P(A) perché ogni insieme è un sottoinsieme improprio di se stesso
Perché c'è anche l'insieme vuoto?
Nella teoria degli insiemi l'insieme vuoto Ø è un sottoinsieme di qualsiasi insieme.
Quindi, l'insieme vuoto Ø è anche un sottoinsieme di A.
Per questo motivo Ø è un elemento dell'insieme delle parti P(A).
L'insieme delle parti dell'insieme vuoto
Nel caso di un insieme vuoto A=Ø l'insieme delle parti è il seguente:
$$ P(A) = \{ Ø \} $$
Devo specificare che {Ø} non è l'insieme vuoto bensì un elemento dell'insieme delle parti.
Perché l'insieme delle parti è detto anche insieme potenza?
L'insieme delle parti si chiama anche insieme potenza per via di una sua proprietà.
Se un insieme A è composto da n elementi, l'insieme delle parti P(A) ha 2n elementi.
Esempio
L'insieme A={a,b} ha n=2 elementi.
L'insieme delle parti P(A) è composto da 2n=22=4 elementi.
Il numero di sottoinsiemi di un insieme con n elementi
Un insieme \( A \) con \( n \) elementi ha \( 2^n \) sottoinsiemi possibili.
Per costruire un qualsiasi sottoinsieme \( X \) in un insieme \( A \) con \( n \) elementi, devo prendere in considerazione ogni elemento di \( A \) e decidere se esso deve appartenere a \( X \) oppure no.
Poiché ogni elemento di \( A \) ha due sole opzioni, essere incluso oppure escluso, il numero totale di combinazioni possibili è il prodotto delle scelte per ciascuno degli \( n \) elementi. Questo porta alla formula:
\[ 2 \cdot 2 \cdot ... \cdot 2 = 2^n \]
Dove il fattore \( 2 \) viene moltiplicato per sé stesso \( n \) volte, una per ogni elemento di \( A \).
Nota. Questa formula include tutti i possibili sottoinsiemi, compresi l'insieme vuoto (che non contiene alcun elemento) e l'insieme stesso (che contiene tutti gli elementi di \( A \)).
Esempio 1
Considero un insieme con \( n = 3 \) elementi.
\[ A = \{a, b, c\} \]
Per conoscere il numero totale dei sottoinsiemi possibili applico la formula:
\[ 2^3 = 8 \]
Quindi, i suoi sottoinsiemi sono otto:
\[ \emptyset, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\} \]
Tra i sottoinsiemi possibili c'è anche l'insieme vuoto $ \emptyset $ e l'insieme intero (o totale) $ A $.
Esempio 2
Se prendo un insieme con \( n = 4 \) elementi, ad esempio:
\[ B = \{1, 2, 3, 4\} \]
Il numero di sottoinsiemi sarà sedici
\[ 2^4 = 16 \]
Anche in questo caso i sottoinsiemi comprendono l’insieme vuoto, i singoli elementi, le coppie, le triplette e l'insieme intero.
Quindi, il calcolo del numero di sottoinsiemi di un insieme finito segue sempre la stessa regola: per un insieme di \( n \) elementi, il numero totale dei suoi sottoinsiemi è dato da \( 2^n \).
E così via.
