Insieme parzialmente ordinato

Un insieme in cui è definito un ordine parziale è detto insieme parzialmente ordinato (A,≤) o in inglese poset (Partially Ordered Set).

Cos'è un ordine parziale?

Dato un insieme A, un ordine parziale è una relazione

$$ ≤:A×A \rightarrow \{ vero, falso \}. $$

tale che dati due elementi dell'insieme (x,y) di A è possibile affermare se la relazione d'ordine ≤ è vera oppure è falsa.

Un esempio pratico

Ho un insieme finito A composto da 7 elementi

$$ A = \{ a, b, c, d, e, f \} $$

Definisco una relazione ≤ tra le coppie AxA degli elementi dell'insieme.

$$ ≤ \{ (a,c,) , (a,e) , (b,d) , (b,f) , (c,g) , (d,g) , (e,g) , (f,g) \} $$

L'insieme (A,≤) è un insieme parzialmente ordinato.

Nota. Non sono le relazioni tra tutti gli elementi dell'insieme ma soltanto tra alcuni. Ad esempio, non ci sono relazioni (a,b) , (a,d) , ecc.

Posso rappresentare graficamente le relazioni dell'insieme parzialmente ordinato (A,≤) in questo modo.

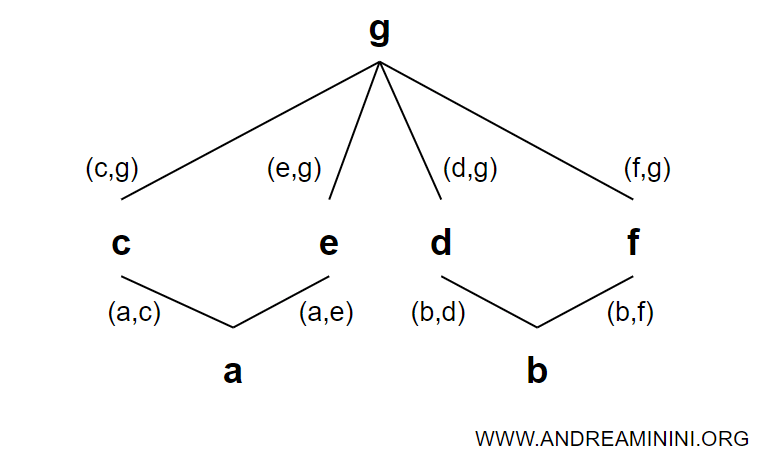
Ogni relazione è rappresentata da un arco che congiunge gli elementi.

Altri esempi di poset

• Numeri naturali
  I numeri naturali formano un poset \( (\mathbb{N}, \leq) \) perché la relazione "minore o uguale" (\(\leq\)) è riflessiva, antisimmetrica e transitiva sui numeri naturali.

  Ad esempio, se prendo due numeri naturali qualsiasi $ \mathbb{N} = \{ 0,1,2,3,... \} $ posso sempre stabilire se un numero è minore-uguale dell'altro oppure no.

• Insieme delle parti di un insieme con inclusione
  Dato un insieme \( S \), l'insieme delle parti di \( S \) che generalmente si indica con il simbolo \( \mathcal{P}(S) \) è un poset (insieme parzialmente ordinato) con la relazione di inclusione (\(\subseteq\)). Sottolineo che in questo caso la relazione d'ordine è l'inclusione e non minore-uguale.
  

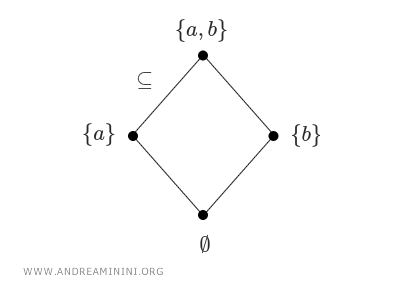
  Ad esempio, se \( S = \{a, b\} \), allora l'insieme delle parti \( \mathcal{P}(S) = \{\emptyset, \{a\}, \{b\}, \{a, b\}\} \) è un poset, dove l'insieme vuoto Ø è incluso in ogni altro insieme, gli insiemi {a} e {b} sono inclusi in {a,b}. Viceversa {a,b} non è incluso né in {a} né in {b}, ecc. $$ \emptyset \subseteq \{ a \} \\ \{ a \} \subseteq \{a,b \} \\ \{ b \} \subseteq \{a,b \} \\ \vdots $$ Posso rappresentare le relazioni di inclusione tra le parti dell'insieme anche con un reticolo, dove i nodi sono i sottoinsiemi mentre gli archi sono le relazioni di inclusione dal basso all'alto.
  

• Divisibilità tra numeri interi
  Un altro poset è formato dall'insieme dei numeri interi \( \mathbb{Z} \) e la relazione di divisibilità "|", dove \( x | y \) significa che x è un divisore di y. In questo caso la relazione d'ordine è la relazione di divisibilità intera.
  

  Ad esempio, se considero i numeri interi x=4 e y=8 , questa coppia soddisfa la relazione di divisibilità x|y perché 4 è un divisore di 8. Viceversa, i numeri x=6 e y=8 non la soddisfano perché 6 non è un divisore di 8. Faccio un esempio completo considerando l'insieme S={2,4,6,8,12,24} e la relazione di divisibilità "|". Nel seguente reticolo (diagramma di Hasse) ogni nodo è un elemento dell'insieme mentre ogni arco o cammino (più archi in sequenza) collega un divisore al dividendo dal basso verso l'alto.
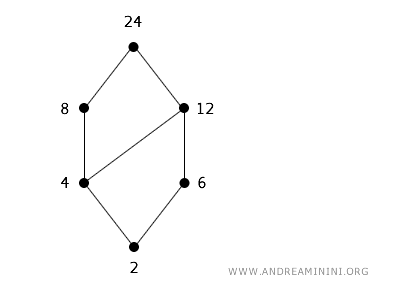  Dove 2 è un divisore di 4,8,6,12,24 ovvero 2|4, 2|8, 2|6, ecc. ma non vale l'inverso. Il numero 6 è un divisore di 12 e 24 ma non di 8, 4 e 2, ecc.

Le proprietà di un poset

Un insieme parzialmente ordinato (poset) è definito da una coppia (S,≤), dove S è un insieme e ≤ è una relazione di ordine su S che per definizione soddisfa tre proprietà fondamentali:

• Riflessività: Ogni elemento è confrontabile con se stesso, ovvero, per ogni x∈S vale x≤x. $$ \forall \ x \in S \ \implies x \leq x $$
• Antisimmetria: Se due elementi sono reciprocamente confrontabili, allora sono uguali, ovvero, se x≤y e y≤x per due elementi x,y∈S, allora x=y. $$ \forall \ x, y \in S, (x \leq y \land y \leq x) \implies x = y $$
• Transitività: Se un elemento è minore di un secondo e questo secondo è minore di un terzo, allora il primo è minore del terzo, ovvero, se x≤y e y≤z per x,y,z∈S, allora x≤z. $$ \forall \ x, y, z \in S, (x \leq y \land y \leq z) \implies x \leq z $$

In altre parole un poset è un insieme dotato di una relazione di ordine che è riflessiva, antisimmetrica e transitiva, ma non necessariamente completa, il che significa che non tutti i membri dell'insieme devono essere comparabili tra loro.

I poset sono fondamentali nella teoria dei reticoli e hanno applicazioni in algebra commutativa, come gli ideali di un anello, e in topologia algebrica.

Gli estremi inferiori e superiori

Dato un insieme parzialmente ordinato (A,≤) e un sottoinsieme B di A

• il sottoinsieme B ha un estremo inferiore inf(B) se esiste un elemento k ∈ A che è il massimo dei minoranti dell'insieme B.
• il sottoinsieme B ha un estremo superiore sup(B) se esiste un elemento k ∈ A che è il minimo dei maggioranti dell'insieme B.

Esempio

Il sottoinsieme B ha sia un estremo inferiore (3) che un estremo superiore (4).

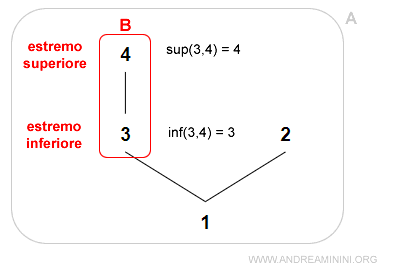
Nota. Non è detto che il sottoinsieme abbia un estremo inferiore o superiore. Tuttavia, se esistono sono unici.

I minoranti e i maggioranti

Dato un insieme parzialmente ordinato (A,≤) e un sottoinsieme B di A

• un elemento k ∈ A è detto minorante del sottoinsieme B se è minore o uguale a ogni elemento del sottoinsieme B.

  Esempio. Dato l'insieme A = {1, 2, 3, 4, 5, 6} e il sottoinsieme B = { 3, 4 }. I minoranti di B sono { 1, 2, 3 }

• un elemento k ∈ A è detto maggiorante del sottoinsieme B se è maggiore o uguale a ogni elemento del sottoinsieme B.

  Esempio. Dato l'insieme A = {1, 2, 3, 4, 5, 6} e il sottoinsieme B = { 3, 4 }. I maggioranti di B sono { 4, 5, 6 }

I massimali e i minimali

Dato un insieme parzialmente ordinato (A,≤)

• un elemento k ∈ A è detto minimale di A se non c'è un altro elemento di A che lo precede.

  Esempio. Dato l'insieme A = {1, 2, 3, 4, 5, 6} il minimale di A è 1.

• un elemento k ∈ A è detto massimale di A se non precede un altro elemento di A.

  Esempio. Dato l'insieme A = {1, 2, 3, 4, 5, 6} il massimale di A è 6.

Un insieme parzialmente ordinato potrebbe anche avere più massimali o più minimali.

Esempio

In questo esempio ci sono tre massimali e un minimale.

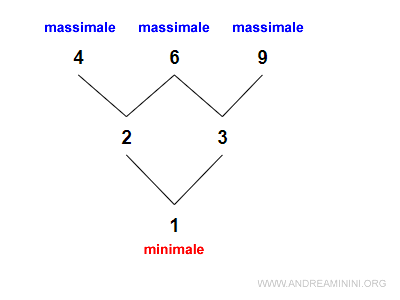
Le relazioni dell'insieme parzialmente ordinato sono le seguenti

$$ ≤ \{ (1,2,) , (1,3), (2,4) , (2,6) , (3,6) , (3,9) \} $$

Posso affermare che

• 4,6,9 non precedono un altro elemento di A. Quindi sono massimali.
• 1 non è preceduto da altri elementi di A. Quindi è minimale.

Nota. Gli insiemi parzialmente ordinati composti da infiniti elementi non è detto che abbiano degli elementi massimali e minimali. Gli insiemi parzialmente ordinati finiti, invece, hanno sempre almeno un elemento massimale e un elemento minimale.

Il massimo e minimo

Dato un insieme parzialmente ordinato (A,≤)

• un elemento k ∈ A è detto minimo di A se è minore o uguale a tutti gli elementi dell'insieme A.
• un elemento k ∈ A è detto massimo di A se è maggiore o uguale a tutti gli elementi dell'insieme A.

Non è detto che gli insiemi parzialmente ordinati abbiano un minimo o un massimo.

Esempio

In questo esempio c'è un minimo (1) ma non un massimo.

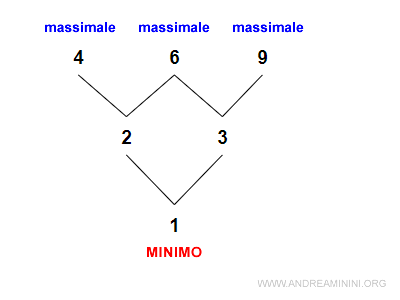
Le relazioni dell'insieme parzialmente ordinato sono le seguenti

$$ ≤ \{ (1,2,) , (1,3) , (2,4) , (2,6) , (3,6) , (3,9) \} $$

Posso affermare che 1 è il minimo perché per ogni elemento k di A vale 1≤k.

$$ 1 \le 2 \\ 1 \le 3 \\ 1 \le 4 \\ 1 \le 6 \\ 1 \le 9 $$

Viceversa non posso affermare che 9 sia il massimo perché mancano le relazioni tra le coppie (2,9), (4,9), (6,9).

$$ 1 \le 9 \\ 3 \le 9 \\ 2 \: ? \: 9 \\ 4 \: ? \: 9 \\ 6 \: ? \: 9 $$

Lo stesso discorso vale per gli altri massimali 4 e 6.

Non posso affermare che 4 sia il massimo perché mancano le relazioni tra le coppie (4,9), (4,6), (4,3).

$$ 1 \le 4 \\ 2 \le 4 \\ 4 \: ? \: 3 \\ 4 \: ? \: 6 \\ 4 \: ? \: 9 $$

Non posso affermare che 6 sia il massimo perché mancano le relazioni tra le coppie (6,4), (6,9).

$$ 1 \le 6 \\ 2 \le 6 \\ 3 \le 6 \\ 4 \: ? \: 6 \\ 9 \: ? \: 6 $$

E così via.