I sottoinsiemi impropri
Cosa sono i sottoinsiemi impropri
Sono detti sottoinsiemi impropri gli insiemi uguali e l'insieme vuoto.
Ogni insieme A ha sempre due sottoinsiemi impropri.
- un insieme identico a se stesso $$ A = A $$
- l'insieme vuoto $$ Ø ⊂ A $$
Insiemi uguali
Considero due insiemi uguali (A=B)
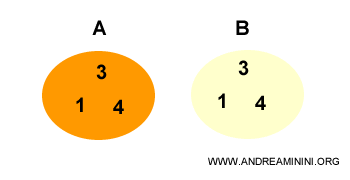
Ogni elemento dell'insieme A è contenuto anche nell'insieme B.
Quindi A è un sottoinsieme di B
$$ A ⊆ B $$
Anche ogni elemento dell'insieme B è contenuto nell'insieme A
Quindi B è un sottoinsieme di A
$$ B ⊆ A $$
Questa particolare relazione di coimplicazione implica l'uguaglianza tra gli insiemi
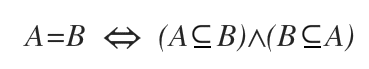
Pertanto, quando due insiemi uguali (A=B) ogni insieme è sottoinsieme dell'altro.
In questi casi si parla di sottoinsieme impropri perché A e B non sono sottoinsiemi propri.
Nota. Un sottoinsieme A è detto sottoinsieme proprio di B se tutti gli elementi di A appartengono anche a B ma esiste almeno un elemento di B che non appartiene ad A. Questa situazione non si verifica quando gli insiemi sono uguali.
Esempio
L'insieme A è incluso nell'insieme B e viceversa
$$ A = \{ 1,3,4 \} $$
$$ B = \{ 1,3,4 \} $$
Ogni elemento dell'insieme A è anche un elemento dell'insieme B e ogni elemento dell'insieme B è anche elemento di A.
Pertanto i due insiemi sono l'uno il sottoinsieme improprio dell'altro.
L'insieme vuoto
Un insieme è detto insieme vuoto se non contiene nemmeno un elemento.
Si indica con il simbolo Ø. $$ Ø = \{ \ \ \} $$
L'insieme vuoto è un sottoinsieme improprio di qualsiasi altro insieme.
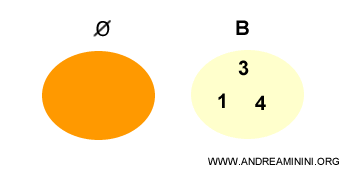
Nota. Il fatto che l'insieme vuoto sia un sottoinsieme di tutti gli altri insiemi è un concetto poco intuitivo ma dimostrabile ( vedi dimostrazione ). Nel prossimo esempio proverò a spiegarlo.
Esempio
Considero l'insieme vuoto e un generico insieme A
$$ Ø = \{ \ \ \} $$
$$ A = \{ 1,3,4 \} $$
L'insieme vuoto Ø è strettamente incluso nell'insieme A
$$ Ø ⊂ A $$
Per dimostrarlo considero vera l'ipotesi contraria per assurdo.
"L'insieme vuoto NON è un sottoinsieme di A"
Allotra dovrebbe esistere almeno un elemento dell'insieme vuoto che non appartiene all'insieme A.
Tuttavia, questa è una contraddizione perché l'insieme vuoto non ha elementi.
Pertanto, l'affermazione "l'insieme vuoto NON è un sottoinsieme di A" è falsa.
Se quest'ultima affermazione è falsa, allora è vera l'affermazione contraria ossia "l'insieme vuoto è un sottoinsieme di A"
Dimostrazione alternativa. L'unione di un insieme A con uno qualsiasi dei suoi sottoinsiemi B⊆A è uguale all'insieme stesso. $$ A \cup B = A $$ Lo stesso accade tra l'unione di un insieme e un insieme vuoto $$ A \cup Ø = \{ 1,3,4 \} \cup \{ \ \ \} = \{ 1,3,4 \} = A $$
