I sottoinsiemi propri

Cosa sono i sottoinsiemi propri

Un insieme A è detto sottoinsieme proprio dell'insieme B quando


• tutti gli elementi di A appartengono anche a B
• almeno un elemento di B non appartiene ad A.

In questi casi si parla di relazione di inclusione stretta.

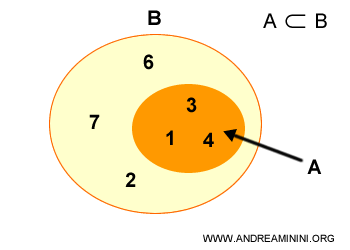
Si tratta di un caso particolare di inclusione. Si indicato con il simbolo ⊂.

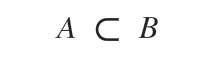
Quest'ultima affermazione si legge "l'insieme A è parte propria dell'insieme B" oppure "l'insieme A è strettamente incluso nell'insieme B".

L'inclusione stretta implica che i due insiemi siano diversi A≠B.

Qual è la differenza tra inclusione normale e inclusione stretta? Nell'inclusione stretta (A⊂B) gli insiemi A e B devono essere diversi (A≠B) perché almeno un elemento di B non appartiene ad A. Viceversa, nell'inclusione normale (A⊆B) gli insiemi possono anche essere uguali (A=B). Pertanto, se è vera l'inclusione stretta (A⊂B) allora è vera anche l'inclusione normale (A⊆B). Viceversa, se è vera l'inclusione normale (A⊆B) non è detto che sia vera anche l'inclusione stretta (A⊂B), perché i due insiemi potrebbero anche essere uguali (A=B).

Esempio

L'insieme A è composto da tre elementi mentre l'insieme B è composto da sei elementi.

$$ A = \{ 1,3,4 \} $$

$$ B = \{ 1,3,4,2,6,7 \} $$

La prima condizione dell'inclusione stretta è soddisfatta perché tutti gli elementi dell'insieme A appartengono anche all'insieme B.

$$ A = \{ 1,3,4 \} ⊂ B $$

Anche la seconda condizione è soddisfatta perché esiste almeno un elemento di B che non appartiene anche ad A

In questo caso ci sono tre elementi {2,6,7} di B che non appartengono ad A

$$ B = \{ 1,3,4,\color{red}2,\color{red}6,\color{red}7 \} $$

Pertanto, l'insieme A è strettamente incluso nell'insieme B ossia l'insieme A è un sottoinsieme proprio di B

$$ A ⊂ B $$

E così via.