La cardinalità degli insiemi

La cardinalità di un insieme $X$ indica il numero di elementi contenuti nell'insieme. Per rappresentarla si usa il simbolo $|X|$

Questo concetto si estende oltre il semplice conteggio degli elementi, specialmente per insiemi di dimensione infinita.

• Cardinalità di insiemi finiti
  La cardinalità di un insieme finito è il conteggio diretto dei suoi elementi.

  Ad esempio, se considero una libreria con una collezione di libri. Se la libreria contiene cinque libri, la cardinalità dell'insieme dei libri è cinque, espressa come $|A| = 5$, dove $A$ è l'insieme dei libri.

• Cardinalità di insiemi infiniti
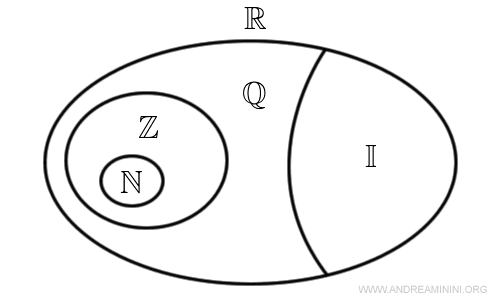
  La situazione si complica con gli insiemi infiniti, i quali possono differire significativamente nella loro grandezza.

  Ad esempio, l'insieme dei numeri naturali $\mathbb{N} = \{ 0,1,2,3,... \}$ e quello dei numeri interi $\mathbb{Z} = \{ ... -2, -1, 0, 1, 2, 3, ... \}$ sono entrambi infiniti e hanno loro cardinalità "numerabile". Ciò significa che è possibile ordinare i loro elementi in una sequenza infinita. Tuttavia, l'insieme dei numeri naturali è un sottoinsieme dell'insieme dei numeri interi $\mathbb{N} \subset \mathbb{Z}$ Un altro insieme infinito è l'insieme dei numeri reali $\mathbb{R}$ che include tutti i punti di una linea continua e presenta una cardinalità "non numerabile" perché tra due punti distinti qualsiasi esistono infiniti altri punti intermedi. Quindi, i numeri interi sono un sottoinsieme dei numeri reali $\mathbb{Z} \subset \mathbb{R}$, il che lo rende un infinito di grandezza superiore a quello di $\mathbb{N}$ o $\mathbb{Z}$.
  

In sintesi, la cardinalità non è solo una misura quantitativa degli insiemi; perché introduce l'idea che esistano diversi ordini di infinito, rivelando una struttura più complessa rispetto a quanto ci appare a prima vista.

Osservazioni

Alcune osservazioni e note a margine

• Cardinalità di insiemi finiti
  Se A e B sono insiemi finiti e A⊆B, allora il numero di elementi (cardinalità) di A è minore o uguale a quelli di B, ovvero ∣A∣≤∣B∣. In altre parole se l'insieme A è un sottoinsieme di B, allora l'insieme A ha un numero minore o uguale di elementi rispetto all'insieme B. $$A \subseteq B \Leftrightarrow |A| \le |B|$$

  Esempio. Ho due insiemi $$A = \{ 1, 2, 3 \}$$ $$B = \{ 1, 2, 3, 4 \}$$ E' evidente che A è un sottoinsieme di B perché tutti i suoi elementi appartengono anche a B $$A \subseteq B$$ L'insieme A è composto da tre elementi, quindi la sua cardinalità è |A|=3 mentre l'insieme B ha quattro elementi e la sua cardinalità è |B|=4. La cardinalità del sottoinsieme A è minore-uguale alla cardinalità dell'insieme B $$|A| \le |B|$$

• Cardinalità di insiemi uguali
  Se A e B sono insiemi uguali $A=B$ allora il numero di elementi di A è uguale a quello di B. Pertanto, i due insiemi hanno la stessa cardinalità $|A|=|B|$. La cardinalità di un insieme indica il numero di elementi contenuti in quell'insieme. Se due insiemi sono uguali, come nel caso degli insiemi $A$ e $B$, la loro cardinalità sarà ovviamente la stessa. $$A = B \Rightarrow |A| = |B|$$

  Esempio. Prendo come esempio due insiemi finiti A e B $$A = \{1, 2, 3\}$$ $$B = \{3, 1, 2\}$$ Entrambi gli insiemi contengono gli stessi elementi, anche se in ordine diverso. Quindi, $A$ e $B$ sono insiemi uguali e possiamo scrivere $A = B$. La cardinalità di $A$ è 3, perché contiene tre elementi unici (1, 2, 3). Analogamente, anche la cardinalità di $B$ è 3 per lo stesso motivo. Pertanto, gli insiemi A e B hanno la stessa cardinalità. $$|A| = |B| = 3$$

E così via.