Gli insiemi uguali

Due insiemi A e B sono insiemi uguali se soddisfano la doppia inclusione $$ A \subseteq B \wedge B \subseteq A $$ In questo caso si scrive $$ A = B $$

Spiegato in modo più semplice, due insiemi A e B sono uguali se A contiene B e B contiene A.

Entrambi gli insiemi sono sottoinsiemi impropri dell'altro.

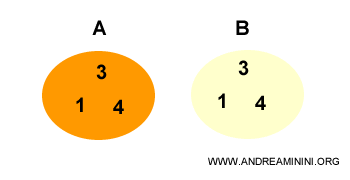
Nota. Ogni insieme ha come sottoinsieme improprio se stesso. È un po' come dire che ognuno è il migliore amico di se stesso. E' tecnicamente vero ...ma non aggiunge molto alla conversazione dal punto di vista sociale.

Dimostrazione

Secondo la prima inclusione tutti gli elementi dell'insieme A appartengono all'insieme B.

$$ A \subseteq B $$

Quindi non esistono elementi di A non contenuti anche in B.

Secondo la seconda inclusione tutti gli elementi dell'insieme B appartengono all'insieme A.

$$ B \subseteq A $$

Pertanto, non esistono elementi di B non contenuti anche in A.

Se non esistono elementi di B non contenuti in A ed elementi di A non contenuti in B, è evidente che i due insiemi sono uguali.

$$ A = B \Leftrightarrow A \subseteq B \wedge B \subseteq A $$

In alternativa, posso anche scrivere che due insiemi sono uguali quando tutti gli elementi di A appartengono anche a B e viceversa. $$ A = B \Leftrightarrow ( x \in A \Leftrightarrow x \in B ) $$

Esempio

Ho due insiemi

$$ A = \{ 0, 1, 2, 3, 4 \} $$

$$ B = \{ x \in N \ | \ 2x + 1 < 10 \} $$

Al secondo insieme B appartengono tutti i numeri naturali che soddisfano la condizione 2x+1<10.

$$ 2x+1<10 $$

$$ x < \frac{9}{2} $$

ossia i numeri naturali 0, 1, 2, 3, 4

$$ A = \{ 0, 1, 2, 3, 4 \} $$

$$ B = \{ 0, 1, 2, 3, 4 \} $$

Come si può notare valgono entrambe le condizioni di inclusione

$$ A \subseteq B $$

$$ B \subseteq A $$

Quindi i due insiemi sono uguali.

$$ A=B $$

Osservazioni

Alcune osservazioni e note a margine sugli insiemi uguali:

• Due insiemi uguali hanno la stessa cardinalità
  Può sembrare ovvio ma a volte è utile ricordarlo. Due insiemi uguali A=B hanno gli stessi elementi, quindi hanno anche lo stesso numero di elementi ovvero hanno la stessa cardinalità. $$ | A | = |B| $$

E così via.