Insieme complemento
Se l'insieme B è un sottoinsieme dell'insieme A $$ B⊆A $$ l'insieme complemento relativo di B rispetto ad A è un insieme composto da tutti gli elementi di A che non appartengono anche a B. $$ A \text{ \ } B = \{ x \in A | x \notin B \} $$ E' anche detto insieme complementare relativo di B rispetto ad A.
Si legge "l'insieme A\B è il complemento dell'insieme B" oppure "A\B è l'insieme complementare di B rispetto ad A".
Ecco il diagramma di Venn.
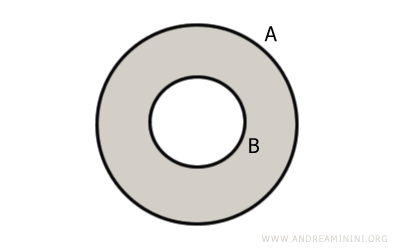
L'area grigia è l'insieme complementare di B rispetto ad A ossia l'insieme A\B.
L'insieme complementare coincide con l'insieme differenza A-B.
Un esempio pratico
Considero due insiemi finiti A e B
$$ A = \{ 2, 4, 6, 8, 10 \} $$
$$ B = \{ 4, 6 \} $$
L'insieme complementare di B rispetto ad A è l'insieme composto dagli elementi di A che non appartengono anche a B
$$ A \text{ \ } B = A-B = \{ 2, 8, 10 \} $$
La rappresentazione grafica tramite i diagrammi di Eulero-Venn è la seguente
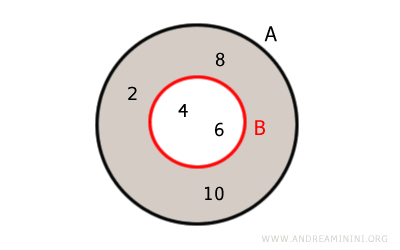
Spiegazione. Gli elementi 4, 6 appartengono sia all'insieme A e sia all'insieme B. Sono gli elementi in comune tra i due insiemi. L'insieme complementare di B rispetto ad A è composto dagli elementi di A non in comune ossia { 2, 8, 10}.
Esempio 2
In questo esempio considero due insiemi infiniti.
L'insieme dei numeri naturali N={1,2,3,4,5,...} e il sottoinsieme dei numeri naturali pari P={2,4,6,8,...}.
$$ N = \{ 1, 2, 3, 4, 5, ... \ \} $$
$$ P = \{ 2, 4, 6, 8, ... \ \} $$
L'insieme complementare di P rispetto a N è l'insieme dei numeri naturali dispari D
$$ N \text{ \ } P = D = \{ 1, 3, 5, 7, 9, ... \ \} $$
L'insieme complementare assoluto
L'insieme complementare assoluto di un insieme A rispetto all'insieme universo U è l'insieme di tutti gli elementi di U che non appartengono ad A. $$ C_A = \{ x \in U | x \notin A \} $$ E' anche detto insieme complementare assoluto di A.
Cos'è l'insieme universo?
L'insieme universo U è l'insieme che comprende tutti gli insiemi con cui si sta lavorando.
Se non specificato diversamente, l'insieme universo è l'insieme che comprende tutti gli insiemi in generale (insieme universale).
Esempio
Considero un insieme A nell'insieme universo U
L'insieme complementare di A ossia CA ( area grigia ) è composto da tutti gli elementi di U che non appartengono ad A ( area bianca ).
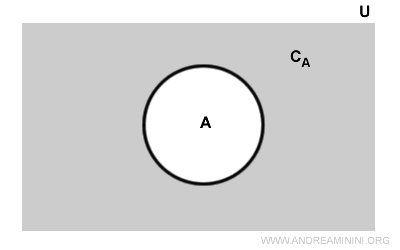
Si dice "l'insieme U\A (o U-A) è il complementare dell'insieme A".
L'insieme complementare U\A è anche indicato con le notazioni U-A, CA, AC, -A,
Osservazioni
Alcune osservazioni utili sugli insiemi complementari
- L'insieme complementare di A rispetto a se stesso è l'insieme vuoto perché A-A=Ø.
$$ A \text{ \ } A = A-A = Ø $$
- Se A e B sono due insiemi uguali A=B, l'insieme complementare di B (o di A) è l'insieme vuoto.
$$ A=B \Longleftrightarrow A-B = Ø $$
- L'insieme complementare dell'insieme vuoto rispetto all'insieme A è uguale all'insieme A perché A-Ø=A
$$ Ø \text{ \ } A = A $$
- L'unione tra l'insieme A e il complemento di A rispetto a B (ossia B\A) è l'insieme universo B
$$ A \cup (B \text{ \ } A) = B $$
- L'intersezione tra l'insieme A e il complemento di A rispetto a B (ossia B\A) è l'insieme vuoto
$$ A \cap (B \text{ \ } A) = Ø $$
E così via.
