Unione di insiemi numerabili

L'unione degli insiemi numerabili è a sua volta un insieme numerabile. $$ A_1 ∪ A_2 ∪ A_3 ∪ ... $$

L'unione può essere composta indifferentemente da un numero finito o infinito di insiemi numerabili.

Dimostrazione

Ho un'infinità di insiemi numerabili A

$$ A_1, A_2, A_3, ... $$

Ogni insieme n-esimo è composto da infiniti elementi

$$ A_n = \{ a_n1, a_n2, a_n3, ... \} $$

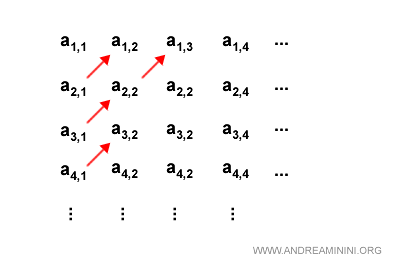
Metto in tabella gli elementi degli insiemi.

Ogni riga contiene gli elementi dell'i-esimo insieme, ogni colonna indica il j-esimo elemento.

$$ a_{11}, a_{12}, a_{13}, a_{14} ... \\ a_{21}, a_{22}, a_{23}, a_{24} ... \\ a_{31}, a_{32}, a_{33}, a_{34} ... \\ a_{41}, a_{42}, a_{43}, a_{44} ... \\ \vdots $$

Posso mettere in relazione tra loro gli elementi della tabella con l'insieme dei numeri naturali in questo modo:

$$ a_{h,k} = k + \sum_{i=1}^{h+k-2} i $$

Dove h e k indicano rispettivamente un numero di riga e di colonna della tabella.

$$ a_{1,1} = 1 + \sum_{i=1}^{0} i = 1 \\ a_{2,1} = 1 + \sum_{i=1}^{1} i = 2 \\ a_{1,2} = 2 + \sum_{i=1}^{1} i = 3 \\ a_{3,1} = 1 + \sum_{i=1}^{2} i = 4 \\ \vdots $$

La successione di elementi è a sua volta un insieme numerabile

$$ a_{1,1}=1 , a_{2,1}=2 , a_{1,2}=3 , a_{3,1}=4 , ... $$

Questo procedimento è detto diagonale di Cantor.

E così via.