Insieme compatto

Più formalmente, in uno spazio topologico, un insieme \(K\) è compatto se per ogni copertura aperta di \(K\), esiste una sottocopertura finita che ancora ricopre \(K\).

Queste definizioni sono equivalenti in \(\mathbb{R}^n\), ma possono divergere in spazi più generali.

Nota. La compattezza garantisce numerose proprietà utili, come il raggiungimento dei massimi e minimi per funzioni continue (Teorema di Weierstrass) e la possibilità di estrarre sottosuccessioni convergenti da qualsiasi successione (Teorema di Bolzano-Weierstrass). In particolar modo, la compattezza garantisce che le funzioni continue definite sull'insieme raggiungono sempre un massimo e un minimo, senza eccezioni.

Esempi pratici

Esempio

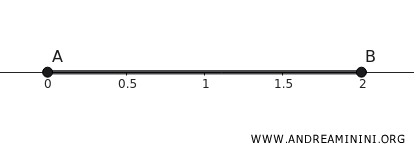
Considero l'intervallo \([0,2]\) nella retta reale \(\mathbb{R}\).

Definisco l'insieme:

\[ K = \{ x \in \mathbb{R} \mid 0 \leq x \leq 2 \} \]

Questo insieme è compatto perché:

• È chiuso: contiene i punti di frontiera \(0\) e \(2\).
• È limitato: tutti i suoi punti stanno fra \(0\) e \(2\), quindi non si estende all'infinito.

Esempio 2

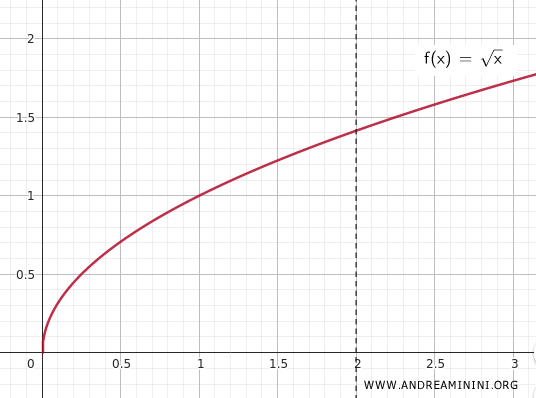
Prendo la funzione continua \(f(x) = \sqrt{x}\) definita su \(K\).

Poiché \(f(x)\) è continua su un insieme compatto, per il teorema di Weierstrass la funzione \(f(x)\) ammette massimo e minimo su \(K\).

Infatti, su \([0,2]\), \(f(x)\) raggiunge il minimo in \(x=0\) (valore \(0\)) e il massimo in \(x=2\) (valore \(\sqrt{2}\)).

Esempio 3

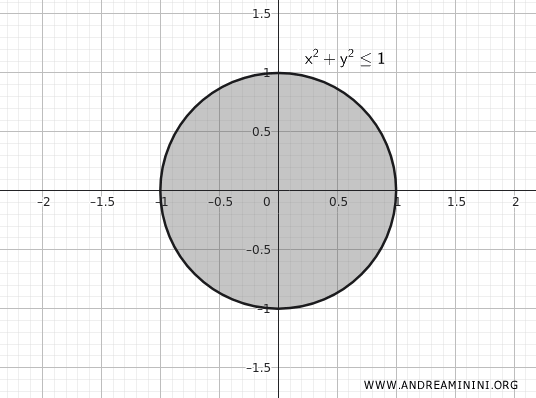
Considero il disco chiuso di raggio \(1\) centrato nell'origine nel piano \(\mathbb{R}^2\).

Definisco l'insieme:

\[ K = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 \leq 1 \} \]

Anche questo insieme è compatto perché:

• È chiuso: include tutti i punti sulla circonferenza (\(x^2 + y^2 = 1\)).
• È limitato: non si allontana oltre distanza \(1\) dall'origine \( (0;0) \).

E così via.