La differenza simmetrica tra insiemi

La differenza simmetrica tra due insiemi A e B è l'insieme degli elementi che appartengono a uno solo dei due insiemi, ma non a entrambi. $$ A \Delta B = (A \setminus B) \cup (B \setminus A) $$

Questa operazione mi permette di identificare gli elementi che appartengono a uno solo dei due insiemi considerati, escludendo quelli comuni.

Formalmente, si esprime come:

$$ A \Delta B = (A \setminus B) \cup (B \setminus A) $$

Dove:

• A\B è l'insieme degli elementi che appartengono ad A ma non a B
• B\A è l'insieme degli elementi che appartengono a B ma non ad A

In altre parole, la differenza simmetrica è l'unione delle differenze relative tra i due insiemi.

E' particolarmente utile per identificare elementi unici tra due insiemi.

Nei diagrammi di Eulero-Venn la differenza simmetrica tra insiemi è rappresentata dalle aree non sovrapposte tra i due cerchi che rappresentano gli insiemi.

Un esempio pratico

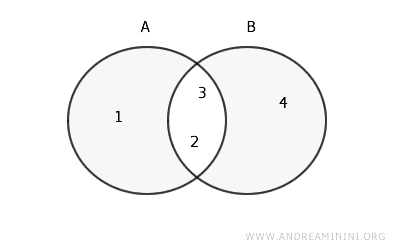
Consideriamo due insiemi A e B.

$$ A = \{1, 2, 3\} $$

$$ B = \{2, 3, 4\} $$

La differenza simmetrica \(A \Delta B\) sarà composta dagli elementi che appartengono a A ma non a B, uniti agli elementi che appartengono a B ma non a A:

$$ A \setminus B = \{1\} $$

$$ B \setminus A = \{4\} $$

Quindi, la differenza simmetrica tra A e B è l'insieme {1, 4}.

$$ A \Delta B = \{1\} \cup \{4\} = \{1, 4\} $$

Dal punto di vista dei diagrammi di Venn

Esempio 2

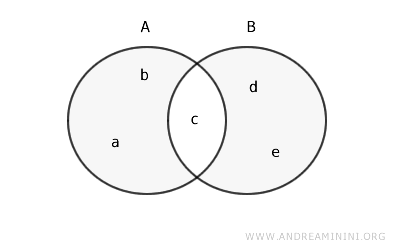
Considero un altro esempio:

$$ A = \{a, b, c\} $$

$$ B = \{c, d, e\} $$

Calcolo la differenza simmetrica \(A \Delta B\):

$$ A \setminus B = \{a, b\}  $$

$$ B \setminus A = \{d, e\} $$

Quindi, la differenza simmetrica tra A e B è l'insieme {a, b, d, e}.

$$ A \Delta B = \{a, b\} \cup \{d, e\} = \{a, b, d, e\} $$

Questa è la rappresentazione con i diagrammi di Eulero-Venn

Le proprietà della differenza simmetrica

La differenza simmetrica gode di diverse proprietà interessanti:

• Commutatività
  L'ordine degli insiemi non altera il risultato. \[ A \Delta B = B \Delta A \]
• Associatività
  Permette di raggruppare gli insiemi in modo diverso senza cambiare il risultato. \[ A \Delta (B \Delta C) = (A \Delta B) \Delta C \]
• Identità
  La differenza simmetrica di un insieme con l'insieme vuoto è l'insieme stesso. \[ A \Delta \emptyset = A \]
• Complementarità
  La differenza simmetrica di un insieme con se stesso è l'insieme vuoto. \[ A \Delta A = \emptyset \]

E così via.