Cardinalità superiore al numerabile

L'insieme delle parti ha cardinalità superiore all'insieme numerabile.

Un esempio pratico

Dato un insieme numerabile A

$$ A=\{ 1, 2, 3, 4, ... \} $$

L'insieme delle parti è l'insieme di tutti i sottoinsiemi possibili dell'insieme A

$$ P(A)=\{ O, \{1\}, \{1,2\}, \{2\}, \{1,2,3\}... \} $$

Esiste un'applicazione 2^A detta funzione caratteristica tale che

$$ 2^A(a) = 1 \:\: se \:\: a \in P(A) $$

$$ 2^A(a) = 0 \:\: se \:\: a \in P(A) $$

Quindi

$$ P(A) ≅ 2^A = \{ f:A \rightarrow \{ 0,1 \} \} $$

Per ogni sottoinsieme S ⊆ A esiste un elemento uguale a S nell'insieme delle parti P(A).

$$ S \in P(A) $$

Quindi, per ogni elemento a di A esiste una corrispondenza con l'insieme P(A) tramite l'applicazione 2^A.

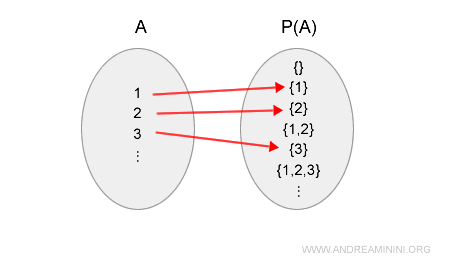
Essendo 2^A un'applicazione iniettiva, deduco che la cardinalità dell'insieme A è inferiore a quella dell'insieme P(A).

$$ Card(A) < Card(P(A)) $$

Pertanto, l'insieme delle parti P(A) ha cardinalità superiore all'insieme numerabile A.

E così via.