L'insieme vuoto

L'insieme vuoto è un insieme senza alcun elemento. Il simbolo dell'insieme vuoto è Ø oppure due parentesi graffe vuote { }.

Il simbolo dell'insieme vuoto, che è rappresentato come ∅, si legge "insieme vuoto" o semplicemente "vuoto". In inglese "empty set".

Un esempio pratico di insieme vuoto

L'insieme dei numeri naturali dispari divisibili per due è un insieme vuoto, perché nessun numero naturale dispari può essere diviso per due.

Esiste un solo insieme vuoto. L'insieme dei numeri naturali dispari divisibili per due è un insieme vuoto. Anche l'insieme dei triangoli con quattro lati è un insieme vuoto. In entrambi i casi si tratta dello stesso insieme vuoto anche se il criterio di appartenenza è diverso. $$ Ø = \{ \ \ \} $$

L'insieme vuoto solleva domande interessanti sulla natura dell'esistenza in matematica, poiché è un'entità che esiste senza contenere alcunché.

Lo potremmo definire il "niente" che è davvero "qualcosa" nel mondo della matematica.

L'insieme vuoto è un sottoinsieme improprio

L'insieme vuoto è un sottoinsieme improprio di ogni insieme.

Dimostrazione

Per dimostrare l'ultima affermazione parto da una dimostrazione per assurdo.

Dato un insieme qualsiasi A, ipotizzo per assurdo che l'insieme vuoto non sia un sottoinsieme di A.

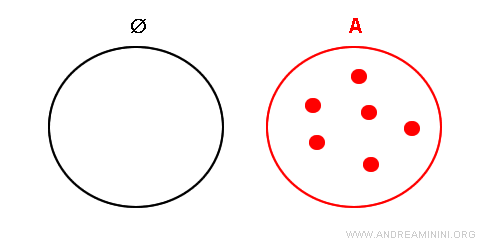
Quindi, dovrebbe esistere almeno un elemento dell'insieme vuoto che non appartiene a A.

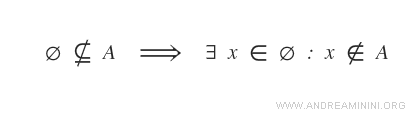
Questo però è impossibile, perché l'insieme vuoto non ha elementi.

Una volta dimostrata la contraddizione di questa ipotesi, allora è vera l'ipotesi contraria, ossia l'insieme vuoto deve essere necessariamente un sottoinsieme di A.

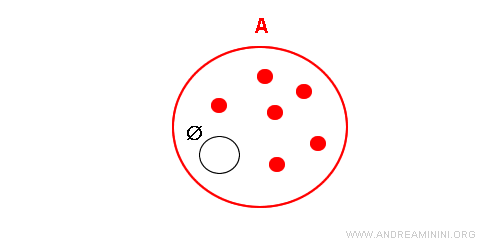
Per questa ragione l'insieme vuoto è considerato un sottoinsieme improprio di qualsiasi altro insieme.

Dimostrazione alternativa. L'unione tra un generico insieme A e uno qualsiasi dei suoi sottoinsiemi B⊆A è sempre uguale all'insieme stesso. $$ A \cup B = A $$ Questo accade anche nell'unione tra l'insieme A e un insieme vuoto $$ A \cup Ø = A $$ Pertanto, anche l'insieme vuoto è un sottoinsieme di A.

Osservazioni

Alcune osservazioni e proprietà dell'insieme vuoto

• L'insieme vuoto è uno e uno solo (unicità)
  Esiste un solo insieme vuoto in matematica. Non importa come o in quale contesto lo utilizzo, l'insieme vuoto è sempre lo stesso. In altre parole, quando si parla dell'insieme vuoto, ci riferiamo sempre allo stesso oggetto matematico.

  Questa unicità è importante perché assicura che tutte le proprietà discusse relative all'insieme vuoto siano universali e non dipendano da una specifica istanza o rappresentazione.  Per questa ragione si parla di "insieme vuoto" al singolare, e non si utilizza mai il plurale (insiemi vuoti).

• L'insieme vuoto è un sottoinsieme di qualsiasi insieme (universalità)
  L'insieme vuoto è un sottoinsieme improprio di ogni altro insieme. Questa è una proprietà universale e molto importante in matematica. Per questa ragione ne parlo in un paragrafo apposito. E' un po' come l'intruso che nessuno ha invitato ma è sempre lì a tutte le feste.

  Per comprendere meglio questa affermazione, possiamo riflettere sul concetto di sottoinsieme. Un insieme \(A\) è un sottoinsieme di un insieme \(B\) se ogni elemento di \(A\) è anche un elemento di \(B\).Nel caso dell'insieme vuoto, \(\emptyset\), non ci sono elementi in esso, quindi la condizione che ogni elemento di \(\emptyset\) debba essere un elemento di un altro insieme \(B\) è sempre soddisfatta, indipendentemente dagli elementi di \(B\). In pratica, non esiste un "controesempio" possibile, perché non ci sono elementi nell'insieme vuoto da considerare.

• Elemento neutrale dell'unione di insiemi
  L'unione tra un insieme A e l'insieme vuoto Ø è ancora l'insieme A, perché l'insieme vuoto non aggiunge alcun nuovo elemento all'insieme A. E' anche detto elemento identità dell'unione di insiemi. $$ A \cup \emptyset = A $$

  Esempio. Considero l'insieme A={a,b,c} e l'insieme vuoto B={ }. L'unione dei due insiemi è sempre l'insieme A. $$ A \cup B = \{ a,b,c \} \cup \{ \ \} = \{a,b,c \} = A $$ $$ B \cup A = \{ \ \} \cup \{ a,b,c \} = \{a,b,c \} = A $$

• Elemento neutrale nella differenza di insiemi
  La differenza tra un insieme A e l'insieme vuoto Ø è sempre l'insieme A perché i due insiemi non hanno elementi in comune. $$ A - \emptyset = A $$

  Esempio. La differenza tra l'insieme A={a,b,c} e l'insieme vuoto B={ } è ancora l'insieme A. $$ A - B = \{ a,b,c \} - \{ \ \} = \{a,b,c \} = A $$ Se invece provo a sottrarre l'insieme A dall'insieme vuoto ottengo ancora l'insieme vuoto perché non ci sono elementi di A da rimuovere nell'insieme vuoto. $$ B-A = \emptyset - A = \{ \ \} -  \{ a, b, c \}  = \{ \ \} = B $$

• Elemento assorbente nell'intersezione degli insiemi
  L'intersezione tra qualsiasi insieme A e l'insieme vuoto Ø è sempre l'insieme vuoto Ø perché non ci sono elementi in comune nei due insiemi. E' detto assorbente perché nell'intersezione con qualsiasi insieme restituisce sempre se stesso. $$ A - \emptyset = A $$

  Esempio. L'intersezione tra l'insieme A={a,b,c} e l'insieme vuoto B={ } è sempre l'insieme vuoto B. $$ A \cap B = \{ a,b,c \} \cap \{ \ \} = \{ \ \} = A $$ $$ B \cap A = \{ \ \}  \cap \{ a,b,c \}  = \{ \ \} = A $$

• Complemento
  Il complemento dell'insieme vuoto in un insieme universo \( U \) è l'universo \( U \) stesso.
  

  Esempio. Considero un insieme universo U e l'insieme vuoto Ø che è un sottoinsieme improprio di qualsiasi insieme. Quindi, il complemento dell'insieme vuoto rispetto all'insieme universo U è l'insieme universo stesso U. $$ U \setminus ∅ = U $$

• Prodotto cartesiano
  Il prodotto cartesiano di qualsiasi insieme A con l'insieme vuoto ∅ è ancora l'insieme vuoto ∅ perché quest'ultimo non ha elementi.

  $$ A \times ∅ = ∅ $$ $$ ∅ \times A = ∅ $$

• Potenza dell'insieme
  L'insieme delle parti o insieme potenza dell'insieme vuoto contiene solo l'insieme vuoto.

  $$ P(∅) = {∅} $$

• L'insieme vuoto è sia aperto che chiuso in topologia
  L'insieme vuoto è considerato sia aperto che chiuso in ogni spazio topologico.
• L'insieme vuoto è un sottoinsieme improprio o proprio?
  In alcuni testi di matematica l'insieme vuoto è definito sottoinsieme improprio. In altri testi, invece, è definito sottoinsieme proprio. Questo accade perché la classificazione dell'insieme vuoto (∅) come sottoinsieme proprio o improprio di un altro insieme può variare a seconda della definizione adottata di "sottoinsieme proprio".

E così via.