La distanza tra insiemi

La distanza tra due insiemi $A$ e $B$ in uno spazio metrico $(X, d)$ è definita come la minima distanza possibile tra un punto di $A$ e un punto di $B$. $$d(A, B) = \inf \{ d(a, b) \mid a \in A \ , \ b \in B$$ dove $d(a, b)$ è la distanza tra due punti $a$ e $b$ secondo la metrica $d$, e $\inf$ (estremo inferioro) rappresenta il più piccolo valore tra tutte queste distanze.

Per trovare la distanza tra due insiemi, prendo ogni possibile coppia di punti, uno in $A$ e uno in $B$, e calcolo la distanza tra ciascuna coppia.

La distanza tra i due insiemi è il valore più piccolo tra tutte queste distanze.

Nota. La distanza tra insiemi misura quanto sono vicini i punti di due insiemi, ma non garantisce che gli insiemi siano uguali o che si tocchino.

Il caso della distanza uguale a zero.

La distanza uguale a zero $d(A, B) = 0$ significa che esistono punti in $A$ e $B$ arbitrariamente vicini, ma non implica necessariamente che $A$ e $B$ si tocchino o abbiano punti in comune.

Quindi, la distanza può essere $0$ anche se gli insiemi sono disgiunti $A \cap B = \emptyset$.

Un esempio pratico

Considero due insiemi A e B in uno spazio metrico composto da tutti i punti della retta e la distanza d=|x₁-x₂|

Poi considero tre casi distinti:

A] Caso 1

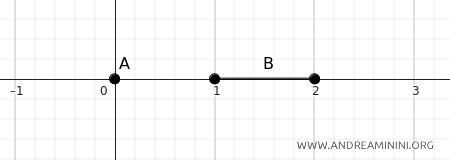
Se $A = \{0\}$ e $B = [1, 2]$ la loro distanza sulla linea retta è uguale a 1.

$$d(A, B) = \inf \{ d(a, b) \mid a \in A, b \in B \} = d(0, 1) = 1$$

In questo caso il punto $0$ di $A$ è a distanza $1$ dal punto più vicino di $B$, ovvero $1$.

B] Caso 2

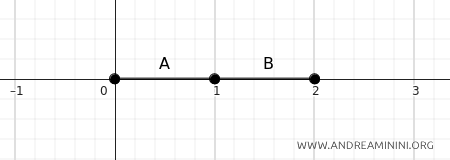
Se $A = [0, 1]$ e $B = [1, 2]$ la loro distanza è zero.

$$d(A, B) = \inf \{ d(a, b) \mid a \in A, b \in B \} = d(1, 1) = 0$$

In questo caso, $A$ e $B$ "toccano" il punto $1$, quindi la distanza è $0$.

I due insiemi non sono disgiunti perché la loro intersezione non è vuota.

$$A \cap B = \{ 1 \}$$

C] Caso 3

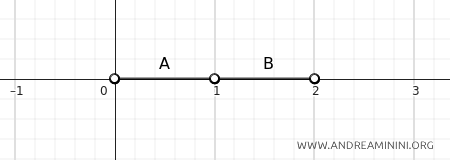
Se $A = (0, 1)$ e $B = (1, 2)$ la loro distanza è zero.

$$d(A, B) = \inf \{ d(a, b) \mid a \in A, b \in B \}.$$

In questo caso i due insiemi sono disgiunti perché sono intervalli aperti e il punto $1$ non appartiene né ad A, né a B... ma la distanza è sempre nulla.

$$A \cap B = \emptyset$$

Questo accade perché per minimizzare la distanza, devo avvicinare $a$ a $1$ (l'estremo destro di $A$) e $b$ a $1$ (l'estremo sinistro di $B$).

Il punto $a$ in $A$ può avvicinarsi arbitrariamente a $1$ ma non raggiungerlo, perché $A$ è aperto.

Allo stesso modo, il punto $b$ in $B$ può avvicinarsi arbitrariamente a $1$ ma non raggiungerlo, perché $B$ è aperto.

Quindi, la distanza tra $A$ e $B$ è:

$$d(A, B) = \inf \{ |a - b| \mid a \in A, b \in B \} = |1 - 1| = 0$$

In conclusione, anche se $A$ e $B$ non si toccano (non hanno punti in comune), esistono punti in $A$ e $B$ arbitrariamente vicini tra loro.

Per questo motivo, la distanza tra $A$ e $B$ è $0$.

Nota. Anche se la distanza tra due insiemi è 0, non significa che i due insiemi siano uguali o che si tocchino. Questo perché la distanza considera punti sempre più vicini, ma non richiede che ci sia un contatto.

E così via.