La collezione di insiemi

Una collezione di insiemi è un insieme i cui elementi sono degli insiemi.

In altre parole, una collezione di insiemi è un insieme di insiemi.

E' un concetto utilizzato in vari rami della matematica, come la teoria degli insiemi, la topologia e l'algebra astratta.

A cosa serve? Una collezione di insiemi può essere utilizzata per definire strutture matematiche più complesse o per esaminare le relazioni tra insiemi diversi.

Ecco alcuni esempi di collezioni di insiemi:

• Famiglia di insiemi
  E' una collezione di insiemi dove gli insiemi hanno qualche proprietà in comune o soddisfano certi criteri. Ad esempio, la famiglia di tutti gli insiemi aperti in uno spazio topologico.
• Partizione di un insieme
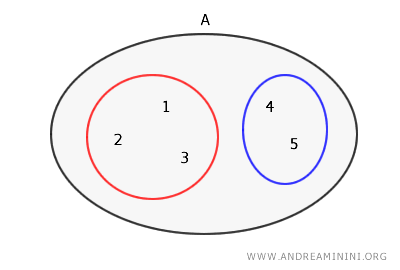
  La partizione di un insieme è una collezione di insiemi disgiunti, tali che l'unione di tutti questi insiemi è l'intero insieme originale. Ogni elemento dell'insieme originale appartiene a uno degli insiemi nella partizione.

  Ad esempio, dato un insieme A={1,2,3,4,5}, una partizione dell'insieme A potrebbe essere una collezione che include come elementi i sottoinsiemi { {1,2,3} , {4,5} }
  

• Potenza di un insieme (insieme delle parti)
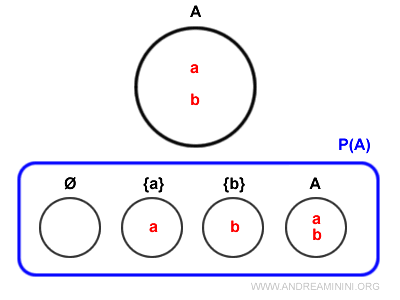
  E' una collezione che comprende tutti i possibili sottoinsiemi di un dato insieme, inclusi l'insieme vuoto e l'insieme stesso.

  Ad esempio, dato un insieme A={a,b} composto da due elementi, l'insieme delle parti P(A) è una collezione di quattro insiemi: { {}, {a}, {b}, {a,b} }
  

Questi concetti sono fondamentali per comprendere e lavorare con le strutture matematiche in modo più dettagliato e per esplorare le relazioni e le proprietà degli insiemi in diversi contesti matematici.