Le relazioni matematiche
Cos'è una relazione
Una relazione è una legge che associa a qualche elemento dell'insieme A uno o più elementi dell'insieme B. $$ aRb $$ Dove a∈A e b∈B e l'elemento b è detto immagine di a.
Da notare ho scritto "qualche" elemento perché non occorre che la legge riguardi tutti gli elementi dell'insieme A.
Non è nemmeno necessario che riguardi tutti gli elementi dell'insieme B.
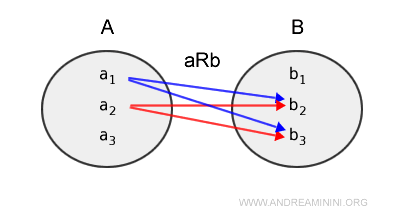
Un elemento dell'insieme A può essere in relazione anche con più elementi dell'insieme B.
Il diagramma di Venn precedente posso rappresentarlo anche in questo modo
Pertanto, la relazione è un sottoinsieme del prodotto cartesiano AxB tra i due insiemi.
$$ R \subseteq AxB $$
Nota. Quando l'insieme A è uguale all'insieme B, ossia A=B, la relazione matematica si dice relazione è definita su A.
Un esempio pratico
Ho due insiemi A e B
$$ A = \{ 2, 4, 6, 8 \} \\ B = \{ 1, 3, 5 \} $$
Il prodotto cartesiano AxB è l'insieme formato da tutte le coppie (a,b) dove a∈A e b∈B.
Ho una relazione R che individua le coppie di elementi (a,b) tali che a+2b<10.
Ad esempio, la coppia (a,b)=(2,1) soddisfa la relazione R perché 2+2·1=4<10
Nota. La coppia di elementi (a,b) appartiene al prodotto cartesiano degli insiemi AxB. Per questa ragione, una relazione è un sottoinsieme del prodotto cartesiano degli insiemi.
La relazione R individua soltanto un sottoinsieme del prodotto cartesiano AxB
Le coppie (2,1), (2,3), (4,1) e (6,1) soddisfano la relazione R mentre le altre no.
Quindi il sottoinsieme aRb è composto da quattro elementi.
$$ aRb = \{ (2,1), (2,3), (4,1) , (6,1) \} \subset AxB $$
Nota. Ovviamente, esistono infinite relazioni tra l'insieme A e B e questa è soltanto una tra le tante. Ad esempio, se la relazione R' è 2a+b<10, il sottoinsieme aR'b è completamente diverso dal precedente. $$ aR'b = \begin{Bmatrix} (2,1) & ( 2,3 ) & (2,5) \\ (4,1) & - & - \\ - & - & - \\ - & - & - \end{Bmatrix} $$
c
Esempio
Riprendo gli insiemi A e B e la relazione R:a+2b<10
Gli elementi dell'insieme A che soddisfano la relazione sono 2, 4, 6
Pertanto, il dominio di R è composto dagli elementi 2, 4, 6 dell'insieme A e il codominio di R dagli elementi 1, 3 dell'insieme B.
$$ \text{dom(R)} = \{2, 4, 6 \} $$
$$ \text{codom(R)} = \{1,3 \} $$
Nota. Nei testi di matematica in cui il dominio è l'insieme di partenza A senza distringuere tra gli elementi che hanno o meno un'immagine in B tramite la relazione R il dominio è composto da tutti gli elementi di A. $$ \text{dom(R)} = \{2, 4, 6, 8 \} $$ In questo caso il sottinsieme di A in cui la relazione R è effettivamente definita è detto insieme di definizione o campo di esistenza di R. $$ \text{insieme di definizione} = \{2, 4, 6 \} $$
La rappresentazione di una relazione
Esistono diversi modi per rappresentare una relazione binaria tra due insiemi
- La rappresentazione per elencazione
Le coppie ordinate (a;b) che soddisfano la relazione sono elencate una dopo l'altra $$ aRb = \{ (2;1), (2;3), (4;1), (6;1) \} $$ - La rappresentazione grafica o sagittale (o diagramma a frecce)
E' la classica relazione tra due insiemi tramite una freccia che collega un elemento dell'insieme A a un elemento dell'insieme B.
- La matrice della relazione (o tabella a doppia entrata)
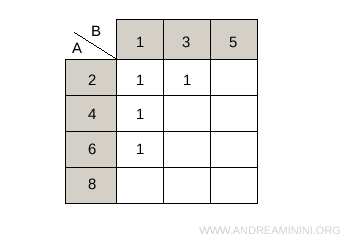
Posso rappresentare la relazione anche con una tabella, detta matrice della relazione, indicando gli elementi a sulle righe e gli elementi b sulle colonne.Nelle celle in cui si incrociano le righe e le colonne inserisco- 1 se la coppia (a,b) soddisfa la relazione R.
- 0 se la coppia (a,b) non soddisfa la relazione R
Un esempio pratico. Il prodotto cartesiano AxB è il seguente:
Per rappresentare la relazione aRb che rispetta la condizione a+2b<10 scrivo la seguente matrice di relazione dove gli elementi del primo insieme A sono disposti in verticale (righe) mentre quelli del secondo insieme B in orizzontale (colonne). $$ aRb = \begin{Bmatrix} 1 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{Bmatrix} $$ In una forma meno matematica ma più comprensibile posso rappresentare la matrice anche tramite una tabella a doppia entrata.
-
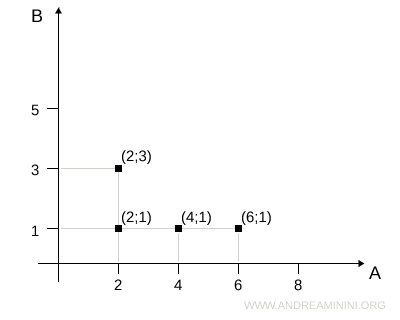
La rappresentazione grafica cartesiana
In un diagramma cartesiano gli elementi del primo insieme (dominio) sono disposti sull'asse orizzontale mentre quelli del secondo insieme (codominio o immagine) sull'asse verticale. I punti del piano indicano le coppie ordinate (a;b) che soddisfano la relazione.
La relazione inversa
Data una relazione b=R(a) la relazione inversa a=R-1(b) collega gli elementi b dell'insieme B agli elementi a dell'insieme A.
Una relazione inversa bR-1a esiste se e solo se esiste la relazione aRb
$$ bR^{-1}a \Leftrightarrow aRb $$
Pertanto, il dominio della relazione inversa R-1 coincide con il codominio della relazione R
$$ dom \ R^{-1} = codom \ R $$
Inoltre, il codominio della relazione inversa R-1 coincide con il dominio della relazione R.
$$ codom \ R^{-1} = dom \ R $$
Un esempio pratico
Riprendo gli insiemi A e B e la relazione R:a+2b<10
Gli elementi dell'insieme A che soddisfano la relazione sono 2, 4, 6
La relazione da A a B è la seguente
$$ aRb = \{ (2,1), (2,3), (4,1) , (6,1) \} \subset AxB $$
La relazione inversa da B ad A è la seguente
$$ bR^{-1}a = \{ (1,2), (3,2), (1,4) , (1,6) \} \subset BxA $$
Il verso della relazione inversa è opposto alla precedente.
Nota. Nella relazione aRb le coppie sono (a,b). Nella relazione inversa le coppie sono in ordine inverso ossia (b,a).
Tipi di relazioni
Esistono tre tipologie di relazioni.
- Le funzioni ( applicazioni )
- Le relazioni binarie
Una relazione binaria fra due insiemi A e B è un sottoinsieme del prodotto cartesiano AxB. Si indica con la notazione $$ aRb \ \ a \in A \ \ b \in B $$ L' Si chiama relazione binaria perché mette in relazione gli elementi di due insiemi. La relazione binaria genera delle coppie di elementi (a;b) $$ (a;b) \in aRb $$ - Le relazioni d'ordine
Sono relazioni riflessive, antisimmetriche e transitive. - Le relazioni di equivalenza
Sono relazioni riflessive, simmetriche e transitive. - Le relazioni di compatibilità
Sono relazioni riflessive, simmetriche, non transitive
Ogni tipologia di relazione ha proprietà peculiari che la distinguono dalle altre.
- Una relazione è riflessiva se $$\forall a \in A \Rightarrow (a,a) \in R $$
- Una relazione è simmetrica se $$ \forall (a,b) \in R \Rightarrow (b,a) \in R $$
- Una relazione è antisimmetrica se $$ \forall (a,b) \in R ∧ (b,a) \in R \Rightarrow a=b $$
- Una relazione è transitiva se $$ \forall (a,b) \in R ∧ (b,c) \in R \Rightarrow (a,c) \in R $$
La proprietà riflessiva, simmetrica e transitiva sono indipendenti tra loro.
Pertanto, esistono relazioni in cui alcune proprietà sono soddisfatte e altre no.
Le proprietà di una relazione R da A in A sono soddisfatte anche nella relazione inversa R-1 se la relazione possiede una qualsiasi tra le seguenti proprietà: riflessiva, simmetrica, antisimmetrica, transitiva.
E così via.
