Il prodotto cartesiano
Il prodotto cartesiano è un'operazione tra due insiemi.
La definizione
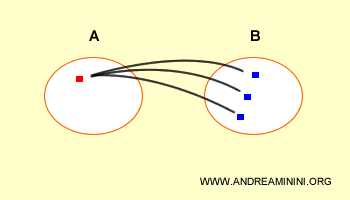
Dati due insiemi A e B, il prodotto cartesiano AxB è l'insieme di tutte le coppie ordinate (a,b) dove il primo elemento "a" appartiene all'insieme A e il secondo elemento "b" appartiene all'insieme B.
Utilizzando la notazione matematica il prodotto cartesiano è definito nel seguente modo:
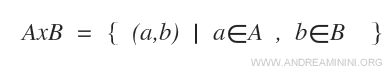
Si legge "A per B" oppure "A cartesiano B".
Un esempio pratico
Per il calcolo del prodotto cartesiano preferisco fare un esempio pratico.
Prendo in considerazione due insiemi A e B composti da due e tre elementi.
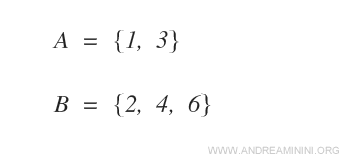
Il prodotto cartesiano AxB è il seguente insieme:
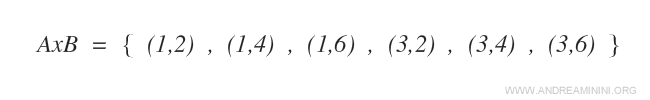
Ogni elemento dell'insieme del prodotto cartesiano AxB è una coppia ordinata.
Dal punto di vista grafico i due insiemi sono legati da queste relazioni.
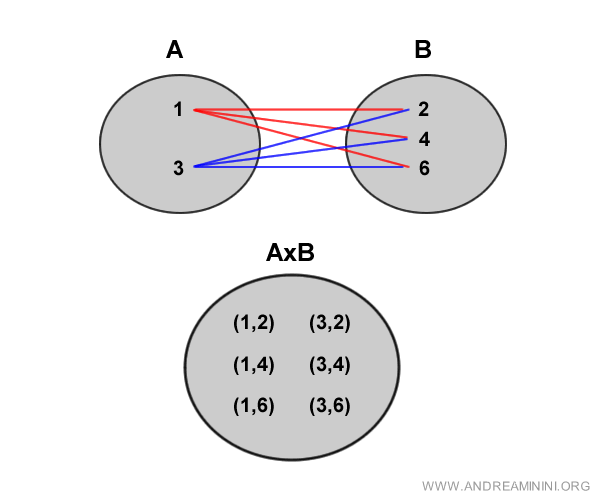
Nota. Gli elementi del prodotto cartesiano non appartengono agli insiemi A o B perché hanno un'altra natura, sono coppie di elementi di A e B.
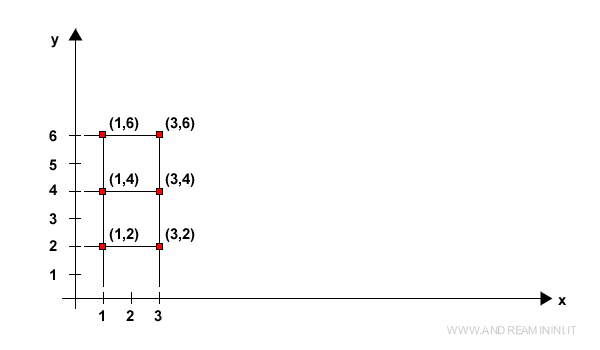
Le coppie ordinate del prodotto cartesiano possono essere rappresentate come coordinate (x,y) su un diagramma cartesiano.
La rappresentazione del prodotto cartesiano
Posso rappresentare il prodotto cartesiano tramite
- Il diagramma cartesiano
Disegno un diagramma cartesiano indicando gli elementi dell'insieme A sull'ascissa (asse orizzontale) e quelli dell'insieme B sull'ordinata (asse verticale). Ogni coppia (a;b) del prodotto cartesiano (AxB) è associata a uno e un solo punto del piano cartesiano (x;y) in cui x=a e y=b.

- Una tabella a doppia entrata
Sulle righe della tabella indico gli elementi del primo insieme (A) del prodotto cartesiano AxB. Sulle colonne della tabella indico gli elemento del secondo insieme (B) del prodotto cartesiano AxB. Nelle celle della tabella (o matrice) inserisco la coppia ordinata (a;b) dei relativi elementi della riga e della colonna.
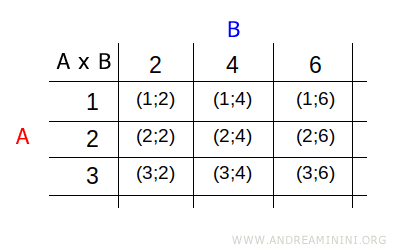
Nota. La rappresentazione tabellare del prodotto cartesiano AxB è utile quando gli elementi di uno o entrambi gli insiemi non sono numeri.
- Diagramma ad albero
Il prodotto cartesiano può essere visualizzato come un albero dove la "radice" (root) rappresenta il punto di partenza. Ogni elemento di \( A \) genera una ramificazione. - Da ogni nodo generato da \( A \), si sviluppano nuove ramificazioni corrispondenti agli elementi di \( B \). - I punti terminali dell’albero (detti "foglie") rappresentano le coppie \((a, b)\) del prodotto cartesiano \( A \times B \).
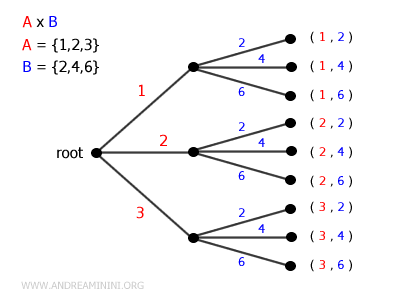
Nota. Se estendo questa rappresentazione a più insiemi \( A_1, A_2, \dots, A_k \), l’albero cresce in profondità. Ad ogni livello, il numero di ramificazioni corrisponde agli elementi dell’insieme corrispondente. - Le foglie finali rappresentano le k-uple ordinate \((a_1, a_2, \dots, a_k)\). Questa visualizzazione è molto utile in informatica, ad esempio per rappresentare gli spazi di ricerca, gli automi e le strutture ad albero.
Cos'è una coppia ordinata?
Una coppia ordinata (a,b) è una coppia di oggetti dove a è il primo elemento e b il secondo elemento.
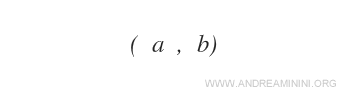
Per indicare una coppia ordinata si utilizzano le parentesi tonde con gli elementi separati da una virgola.
Gli elementi a e b non devono essere necessariamente diversi.
L'ordine degli elementi è importante
In una coppia ordinata l'ordine degli elementi è di fondamentale importanza
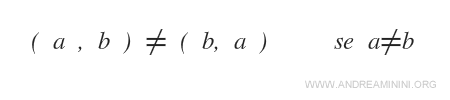
Esempio
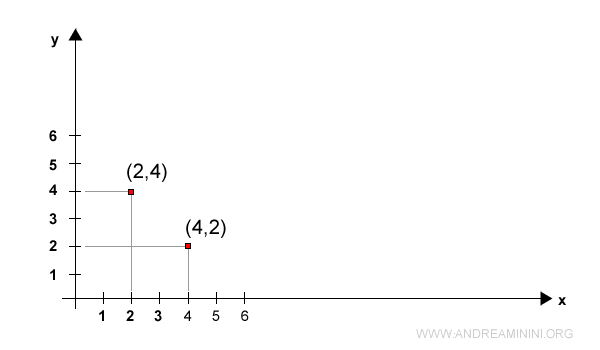
Le coppie ordinate (2,4) e (4,2) sono diverse. Hanno gli stessi valori ma sono disposti in ordine differente.
Le due coppie ordinate indicano due coordinate diverse del piano cartesiano (x,y).
Quando due coppie ordinate sono uguali?
Date due coppie ordinate (a,b) e (c,d) le coppie sono uguali soltanto quando il primo elemento della prima coppia è uguale al primo elemento della seconda coppia (a=c) e il secondo elemento della prima coppia è uguale al secondo elemento della seconda coppia (b=d).
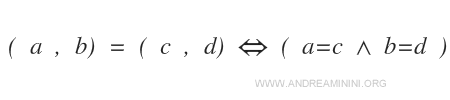
La proprietà commutativa del prodotto cartesiano
Il prodotto cartesiano non gode della proprietà commutativa.
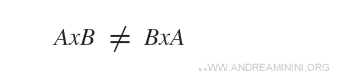
Esempio
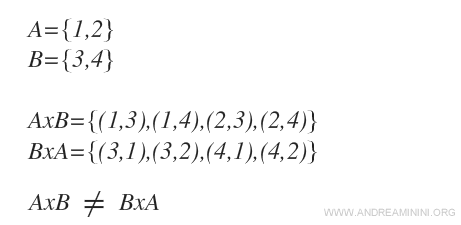
E' evidente che AxB ≠ BxA perché, a differenza di un insieme, in una coppia ordinata l'ordine degli elementi è importante.
La differenza è ben evidente se rappresento i due prodotti cartesiani in un diagramma cartesiano.
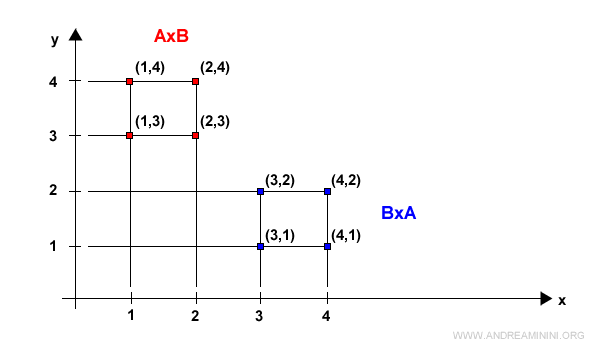
Nota. L'unico caso in cui AxB = BxA è quando A=B. Quando i due insiemi A,B sono identici, il prodotto cartesiano rispetta la proprietà commutativa.

La proprietà distributiva
Il prodotto cartesiano tra due insiemi rispetta la proprietà distributiva rispetto all'unione e all'intersezione
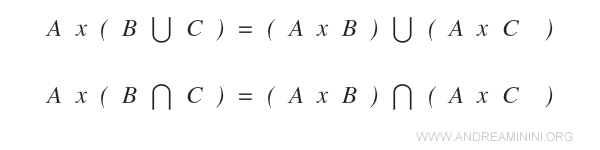
Dimostrazione

Il prodotto cartesiano di un insieme vuoto
Quando uno dei due insiemi del prodotto cartesiano è un insieme vuoto, il prodotto cartesiano dà come risultato un insieme vuoto.
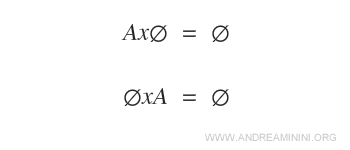
Il prodotto cartesiano di n insiemi
Il prodotto cartesiano è un'operazione che può essere effettuata anche tra n insiemi, non solo tra due insiemi.
Dati n insiemi A1,A2,...,An il prodotto cartesiano A1xA2x...xAn è l'insieme composto dalle n-ple ordinate (a1,a2,...,an). $$ A_1\:x\:A_2\:x\:...\:x\:A_n = \{ (a_1,a_2,...,a_n) | a_i \in A_i , =1,2,...,n \} $$
Dove a1 è un elemento dell'insieme A1, a2 dell'insieme A2, e così via.
In questo caso gli elementi del prodotto cartesiano sono k-uple ordinate (cioè tuple con \( k \) elementi). Ogni coordinata della k-upla proviene da un insieme diverso.
Esempio
Considero tre insiemi A, B, C
$$ A = \{1,2\} $$
$$ B = \{a,b,c\} $$
$$ C = \{X,Y\} $$
il loro prodotto cartesiano sarà:
\[ A \times B \times C = \{ (1,a,X), (1,a,Y), (1,b,X), (1,b,Y), (1,c,X), (1,c,Y), (2,a,X), (2,a,Y), (2,b,X), (2,b,Y), (2,c,X), (2,c,Y) \} \]
Il numero totale di elementi nel prodotto cartesiano è il prodotto delle cardinalità degli insiemi:
\[ |A \times B \times C| = |A| \cdot |B| \cdot |C| = 2 \cdot 3 \cdot 2 = 12 \]
In questo caso nel prodotto cartesiano ci sono 12 triple ordinate.
Quindi, il prodotto cartesiano si può estendere facilmente anche a più insiemi, e il numero di elementi risultante è sempre il prodotto del numero di elementi dei singoli insiemi.
Il prodotto cartesiano di un insieme per se stesso
Il prodotto cartesiano può essere calcolato anche su un insieme per se stesso.
Se prendo lo stesso insieme \( A \) e faccio il prodotto cartesiano \( k \) volte con sé stesso, ottengo:
\[ A^k = A \times A \times \dots \times A \]
Gli elementi di \( A^k \) sono tutte le possibili k-uple ordinate di elementi di \( A \). Se \( A \) ha \( n \) elementi, allora:
\[ |A^k| = n^k \]
Esempio
Considero l'insieme A
$$ A = \{ 1,2,3 \} $$
Il prodotto cartesiano A×A è l'insieme delle coppie ordinate
$$ A×A = \{ (1;1) , (1;2), (1;3), (2;1), (2;2), (2;3), (3;1), (3;2), (3;3) \} $$
Il prodotto cartesiano contiene 9 coppie ordinate perché l'insieme A ha $ n = 3 $ elementi.
\[ |A^2| = 3^2 = 9 \]
Spesso, invece del simbolo A×A, a volte si usa il simbolo A2.
$$ A^2 = A×A = \{ (1;1) , (1;2), (1;3), (2;1), (2;2), (2;3), (3;1), (3;2), (3;3) \} $$
Il significato è sempre lo stesso.
Esempio 2
Considero l'insieme \( A = \{0,1\} \) e \( k = 3 \), in questo caso il prodotto cartesiano \( A^3 \) contiene:
\[ A^3 = A×A×A = \{ (0,0,0), (0,0,1), (0,1,0), (0,1,1), (1,0,0), (1,0,1), (1,1,0), (1,1,1) \} \]
In questo caso il prodotto cartesiano contiene 8 coppie ordinate perché l'insieme A ha $ n = 2 $ elementi.
\[ |A^3| = 2^3 = 8 \]
In generale, lo stesso discorso vale per qualsiasi prodotto cartesiano di un insieme per se stesso per k volte.
Note
Alcune note aggiuntive sul prodotto cartesiano.
- Se l'insieme \( A \) ha \( n \) elementi e l'insieme \( B \) ha \( m \) elementi, allora ogni elemento di \( A \) può essere associato con ciascun elemento di \( B \), generando esattamente \( n \cdot m \) coppie. Quindi, il numero di elementi di \( A \times B \) è: \[ |A \times B| = |A| \cdot |B| = n \cdot m \]
Nota. Questa proprietà si estende a più insiemi: se ho \( k \) insiemi \( A_1, A_2, \dots, A_k \) con rispettivamente \( n_1, n_2, \dots, n_k \) elementi, allora il loro prodotto cartesiano ha \( n_1 \cdot n_2 \cdot \dots \cdot n_k \) elementi.
E così via
