Il limite notevole della potenza
Il limite notevole della potenza kn per n→∞ si dimostra a seconda del valore di k $$ \lim_{n \rightarrow ∞} k^n = \begin{cases} +∞ \:\:\: \text{se k>1} \\ 1 \:\:\: \text{se k=1} \\ 0 \:\:\: \text{se -1<k<1} \\ \text{non esiste} \:\:\: \text{se k ≤ -1} \end{cases} $$
Caso k>1
$$ \lim_{n \rightarrow ∞} k^n $$
Se k>1 si uso la diseguaglianza di Bernoulli.
$$ k^n \ge 1+n(k-1) $$
Essendo k>1, il secondo membro della disequazione diverge a infinito per n tendente a infinito.
$$ \lim_{n \rightarrow ∞} k^n \ge \lim_{n \rightarrow ∞} 1+n(k-1) $$
$$ \lim_{n \rightarrow ∞} k^n \ge ∞ $$
Pertanto, anche il limite della successione kn diverge a infinito per n→∞.
Nota. Ad esempio, se k=1.1
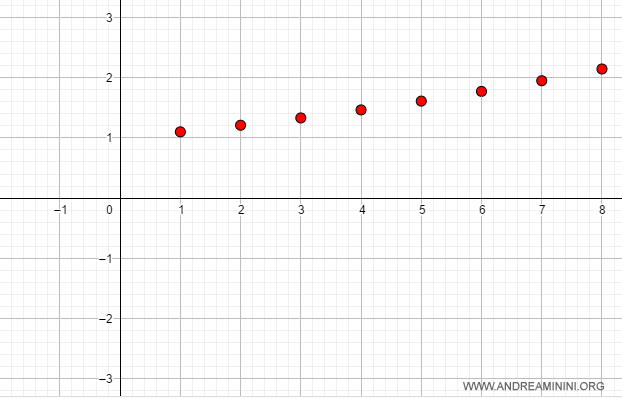
Il limite di una successione è uguale al limite della funzione f(x). Quindi, la dimostrazione è identica.
Caso k=1
$$ \lim_{n \rightarrow ∞} k^n $$
$$ \lim_{n \rightarrow ∞} 1^n $$
Qualsiasi potenza ennesima di 1n è sempre uguale a 1
Quindi il limite della successione converge a 1.
$$ \lim_{n \rightarrow ∞} 1^n = 1 $$
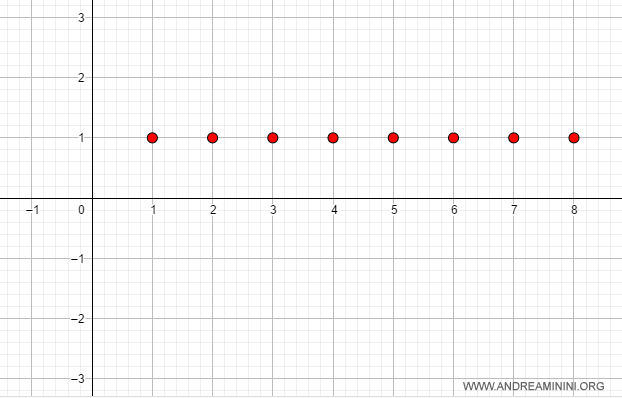
Esempio. La successione converge a 1 per n tendente a infinito.
Caso -1<k<1 con k≠0
$$ \lim_{n \rightarrow ∞} k^n $$
Lo riscrivo in questa forma equivalente
$$ \lim_{n \rightarrow ∞} ( \frac{1}{ \frac{1}{ k} } )^n $$
$$ \lim_{n \rightarrow ∞} \frac{1}{ ( \frac{1}{ k} )^n } $$
La disequazione
$$ -1 < k < 1 $$
posso riscriverla in questa forma
$$ | k | < 1 $$
Divido entrambi i membri per |k|
$$ \frac{ | k | }{|k|} < \frac{1}{|k|} $$
$$ 1 < \frac{1}{|k|} $$
ossia
$$ \frac{1}{|k|} > 1 $$
Pertanto, essendo 1\|k|>1 il denominatore della successione diverge a infinito
$$ \lim_{n \rightarrow ∞} \frac{1}{ ( \frac{1}{ k} )^n } = \frac{1}{∞} = 0 $$
Quindi il limite è uguale a zero per n→∞.
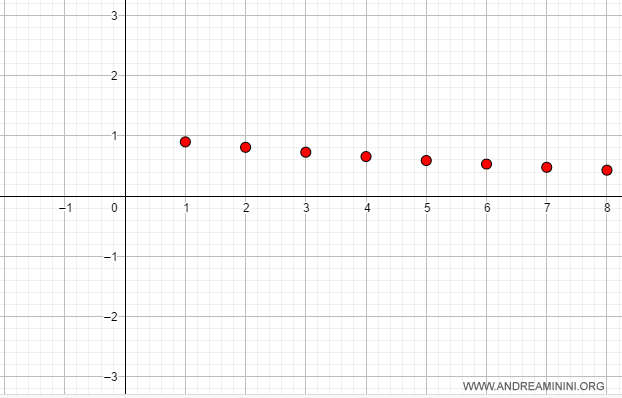
Esempio. Se k=0.9 la successione converge a zero.
Caso k=0
$$ \lim_{n \rightarrow ∞} k^n $$
$$ \lim_{n \rightarrow ∞} 0^n $$
Qualsiasi potenza ennesima di 0n è sempre uguale a 0
Quindi il limite della successione converge a 0.
$$ \lim_{n \rightarrow ∞} 0^n = 0 $$
In quest'ultimo caso la successione è infinitesima.
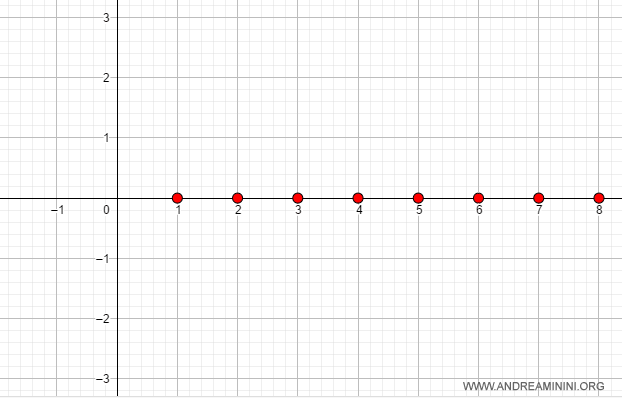
Esempio. Se k=0 la successione converge a zero.
Caso k<-1
$$ \lim_{n \rightarrow ∞} k^n $$
In questo caso, poiché k<-1 la successione diverge.
Tuttavia, la successione diverge a +∞ se n è pari e diverge a -∞ se n è pari.
$$ \lim_{n \rightarrow ∞} k^n = \begin{cases} +∞ \:\: \text{se n è pari} \\ -∞ \:\: \text{se n è dispari} \end{cases} $$
Quindi non esiste un limite per n tendente a infinito
$$ \lim_{n \rightarrow ∞} k^n = \:\: \text{non esiste} $$
Esempio. Se k=-1 la successione oscilla tra 1 e -1. Quindi il limite per n→∞ non esiste.
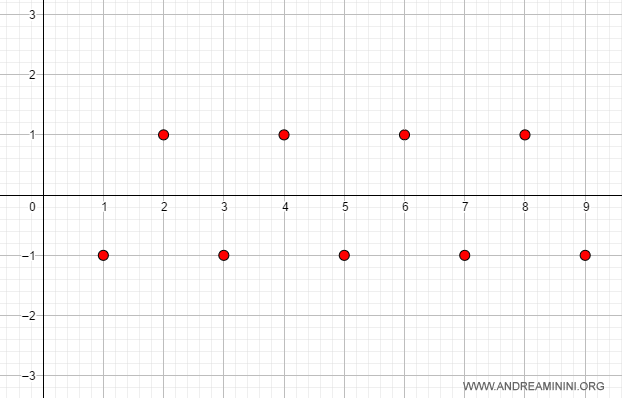
Se k=-1.1 la successione diverge a +∞ quando n è pari e diverge a -∞ quando n è dispari.
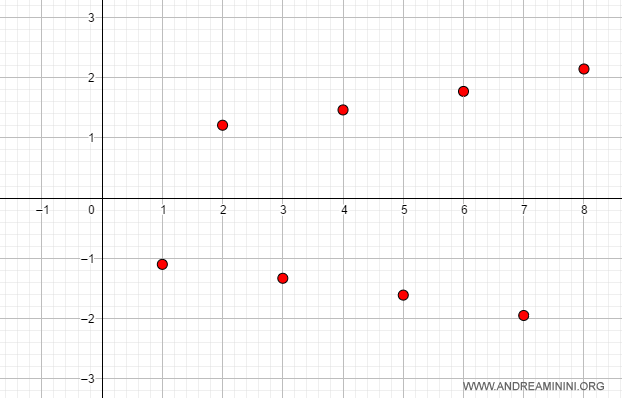
E così via.
