Moto circolare
Il moto circolare è un moto sul piano in cui la traiettoria è una circonferenza.
Esistono due tipi di moti circolari
- Moto circolare vario
La velocità è variabile - Moto circolare uniforme
La velocità è costante
Le coordinate del punto materiale
Può essere descritto in base allo spazio percorso sulla circonferenza s(t) oppure in base all'angolo θ(t) dell'arco.
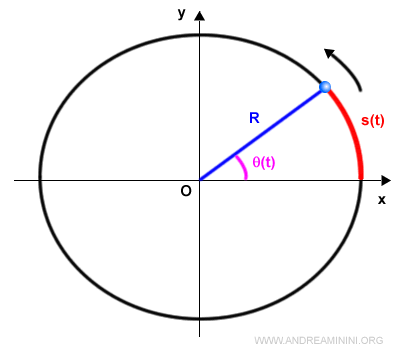
L'angolo e lo spazio percorso sull'arco sono in relazione tra loro.
$$ θ(t) = \frac{s(t)}{R} $$
Dove R è la lunghezza del raggio che congiunge l'origine con il punto P sulla circonferenza.
Essendo la traiettoria una circonferenza, il raggio è costante.
Le coordinate cartesiane del punto materiale durante il moto sono determinate dalle seguenti formule:
$$ x(t) = R \cdot \cos θ(t) $$
$$ y(t) = R \cdot \sin θ(t) $$
Dal punto di vista grafico
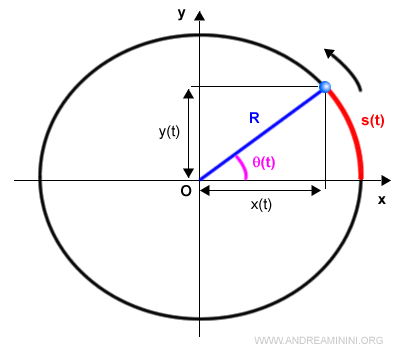
Nota. Il coseno e il seno variano da 1 a -1 con raggio unitario. E' sufficiente moltiplicare le funzioni seno e coseno per un raggio R divero da uno per ottenere le coordinate (x,y) del punto sulla circonferenza.
Come misurare lo spostamento nel moto circolare
Lo spostamento di un punto materiale nel moto circolare può essere misurato in due modi
- La lunghezza dell'arco s(t) percorso sulla circonferenza
- La variazione dell'angolo θ(t)
Nel moto circolare la variazione dell'angolo è la misura preferibile perché è adimensionale, ossia non dipende dalla lunghezza del raggio R.
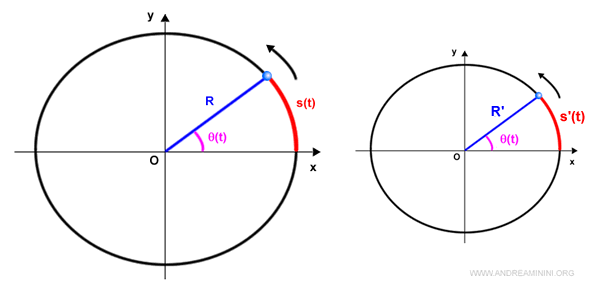
Nota. Lo spazio percorso s(t) sull'arco della circonferenza è influenzato dalla lunghezza del raggio. Ad esempio, due moti circolari con raggio diverso e stesso spazio percorso s(t) hanno velocità di spostamento differenti. Viceversa, due moti circolari con raggio diverso e stesso angolo hanno la stessa velocità di spostamento.
La legge oraria
Il vettore posizione del punto materiale nel moto circolare è
$$ \vec{r(t)} = x(t) \vec{u_x} + y(t) \vec{u_y} $$
Dove x(t) e y(t) sono due scalari moltiplicati per i relativi versori.
Sapendo che
$$ x(t) = R \cdot \cos θ(t) $$
$$ y(t) = R \cdot \sin θ(t) $$
Li sostituisco nella legge oraria e ottengo
$$ \vec{r(t)} = R \cdot \cos θ(t) \vec{u_x} + R \cdot \sin θ(t) \vec{u_y} $$
Nel moto circolare il raggio ha lunghezza costante

La velocità nel moto circolare
La velocità nel moto circolare è il prodotto tra il raggio e la velocità angolare $$ v = R \cdot ω(t) $$
Dimostrazione
La velocità istantanea in punto è la derivata dello spazio percorso s(t) rispetto al tempo (t).
$$ v = \frac{d \: s(t)}{dt} $$
Sapendo che lo spazio percorso s(t) = R·θ
$$ v = \frac{d \: (R \cdot θ) }{dt} $$
Poiché l'angolo varia nel tempo
$$ v = \frac{d \: (R \cdot θ(t)) }{dt} $$
Nel moto circolare il raggio R è costante, posso farlo uscire dalla derivata.
$$ v = R \cdot \frac{d \: θ(t) }{dt} $$
La derivata dθ(t)/dt è la velocità dell'angolo (velocità angolare).
Spesso si indica con il simbolo omega.
$$ ω(t) = \frac{d \: θ(t) }{dt} $$
Quindi, la velocità è il prodotto tra il raggio R e la velocità angolare ω nel tempo.
$$ v = R \cdot ω(t) $$
La notazione vettoriale
Dal punto di vista vettoriale la velocità è pari al prodotto vettoriale (x) tra il vettore della velocità angolare e il raggio vettore r.
$$ \vec{v} = \vec{ω} \: x \: \vec{r} $$
Il risultato del prodotto vettoriale è un vettore ortogonale (normale) ai vettori del prodotto.
Pertanto, la velocità è un vettore ortogonale (90°) al raggio vettore r e alla velocità angolare.
Nota. Poiché la direzione del raggio vettore (r) e del vettore velocità (v) sono tracciate sul piano, ne consegue che la direzione del vettore della velocità angolare esce dal piano in un verso o nell'altro. Solo in questo modo tutti i vettori possono essere ortogonali tra loro.
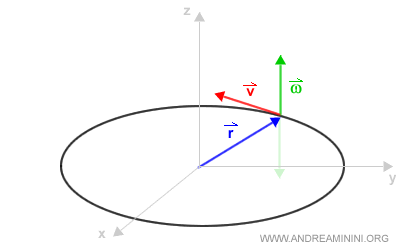
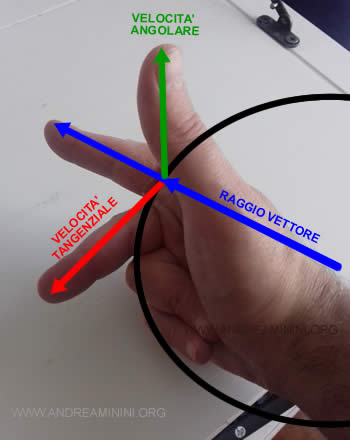
Per capire il verso del prodotto vettoriale (verde) in alto o in basso, posso usare la regola della mano destra. L'indice segue il raggio vettore (blu), il medio segue il vettore velocità (rosso) mentre il pollice indica il verso del prodotto vettoriale (verde) ossia della velocità angolare.
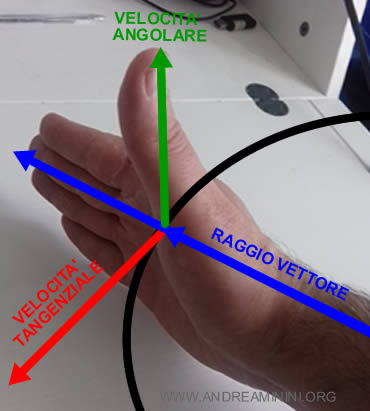
In alternativa, per individuare il verso del prodotto vettoriale (verde) posso indicare il raggio vettore (blu) con la mano destra con il palmo della mano rivolto in direzione della velocità (rossa). Anche in questo modo il pollice individua il verso del prodotto vettoriale (verde) in alto o in basso.
La velocità angolare
La velocità angolare misura la variazione dell'angolo nel tempo. E' anche detta pulsazione (ω).$$ ω = \frac{v}{R} $$ Dove v è la velocità del punto materiale sulla circonferenza e R è il raggio.
La velocità angolare è proporzionale alla velocità del punto materiale sulla circonferenza.
- Se la velocità v è variabile, la velocità angolare ω è variabile.
- Se la velocità v è costante, la velocità angolare ω è costante.
Dimostrazione
La velocità angolare è la derivata dell'angolo rispetto al tempo.
$$ w = \frac{d θ}{dt } $$
Secondo la legge oraria s(t) = R·θ(t)
Quindi, l'angolo θ(t)=s(t)/R
$$ ω = \frac{d [\frac{s}{R} ]}{dt } $$
Il raggio R è una costante ed esce dalla derivata
$$ ω = \frac{1}{R} \frac{d \: s }{dt } $$
La derivata dello spazio percorso sull'arco rispetto al tempo è la velocità del punto materiale v.
$$ ω = \frac{1}{R} \cdot v $$
$$ ω = \frac{v}{R} $$
La formula della velocità angolare è dimostrata.
La velocità radiale e trasversa
Nel moto circolare la velocità radiale è sempre nulla (in modulo) perché il raggio R è costante.
$$ v_r = 0 $$
La velocità trasversa vθ è, invece, uguale alla velocità.
$$ v_θ=v $$
Dal punto di vista grafico
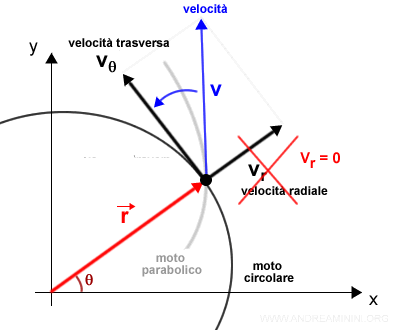
Dimostrazione. Perché la velocità eguaglia la velocità trasversa nel moto circolare? La velocità trasversa è uguale al raggio (r) per la derivata dell'angolo $$ v_θ = r \cdot \frac{d \: θ} {d \: t} $$ Poiché θ(t)=s(t)/R $$ v_θ = r \cdot \frac{d \: [ \frac{s}{R}] } {d \: t} $$ il raggio R è costante ed esce dalla derivata. $$ v_θ = r \cdot \frac{1}{R} \cdot \frac{d \: s } {d \: t} $$ Il raggio r=R è sempre lo stesso e si semplifica $$ v_θ = \frac{d \: s } {d \: t} $$ La derivata dello spazio percorso s rispetto al tempo è la velocità. $$ v_θ = v $$ Ecco dimostrata l'uguaglianza tra la velocità trasversa e la velocità del punto sulla circonferenza.
L'accelerazione nel moto circolare
L'accelerazione vettoriale è composta da due componenti: l'accelerazione tangenziale (aT) e l'accelerazione normale (aN). $$ \vec{a} = \vec{a_T} + \vec{a_N} $$
Per un chiarimento vedere la differenza tra accelerazione tangenziale e normale.
Le componenti a, aT e aN sono vettori.
Per trovare il modulo dell'accelerazione |a| devo ricorrere al teorema di Pitagora.
$$ |a| = \sqrt{a^2_T+a^2_N} $$
Dove l'accerazione tangenziale e l'accelerazione normale sono:
$$ a_T = \frac{d \: v}{dt} $$
$$ a_N = \frac{v^2}{R} $$
Sapendo che v = ω·R
$$ a_T = \frac{d \: (ω \cdot R)}{dt} = R \cdot \frac{d \: ω }{dt} $$
$$ a_N = \frac{(ω \cdot R)^2}{R} = \frac{ω^2 \cdot R^2}{R} = ω^2 \cdot R $$
Pertanto, l'accelerazione tangenziale è il prodotto tra l'accelerazione angolare (dω/dt) e il raggio R.
L'accerazione normale è, invece, il prodotto tra il quadrato velocità angolare e il raggio (ω2R).
La notazione vettoriale
Posso studiare l'accelerazione anche con le grandezze vettoriali.
L'accelerazione vettoriale è la derivata del vettore velocità.
$$ \vec{a} = \frac{d \: \vec{v}}{dt} $$
Il vettore velocità è il prodotto vettoriale tra il vettore della velocità angolare ω e il raggio vettore r ossia v=ω x r.
$$ \vec{a} = \frac{d \: (\vec{ω} x \vec{r})}{dt} $$
Applico la regola di derivazione di un prodotto.
$$ \vec{a} = \frac{d \: \vec{ω} } {dt} \vec{r} + \vec{ω} \frac{d \: \vec{r} }{ dt } $$
La derivata del raggio vettore rispetto al tempo è il vettore velocità v=dr/dt
$$ \vec{a} = \frac{d \: \vec{ ω} }{ dt } \vec{r} + \vec{ω} ( \vec{v} ) $$
Nota. La derivata della velocità angolare rispetto al tempo (dω/dt) è la velocità angolare (α). Pertanto, la precedente equazione si può scrivere anche $$ \vec{a} = α \vec{r} + \vec{ω} \vec{v} $$ che denota una relazione tra l'accelerazione, l'accelerazione angolare e la velocità angolare. Il primo termine (αr) è l'accelerazione tangenziale (aT) il cui modulo è αR mentre il secondo termine (ωv) è l'accelerazione centripeta/normale (aN) il cui modulo è ω2R.
A sua volta il vettore velocità è il prodotto vettoriale della velocità angolare e del raggio vettore r ossia v = ω x r
$$ \vec{a} = \frac{d \: \vec{ ω} }{ dt } \vec{r} + \vec{ω} ( \vec{ω} \vec{r} ) $$
La componente ω(ωr) è un doppio prodotto scalare quindi è pari a ω(ωr)-r(ωω)
$$ \vec{a} =\frac{d \: \vec{ ω} }{ dt } \vec{r} + \vec{ω} (\vec{ω} \vec{r} ) - \vec{r} ( \vec{ω} \vec{ω} ) $$
Nota. Secondo la regola del doppio prodotto scalare tra tre vettori $$ \vec{a} ( \vec{b} \vec{c} ) = \vec{b} ( \vec{a} \vec{c} ) - \vec{c} (\vec{a} \vec{b} ) $$
Il prodotto vettoriale ωr=0 perché i due vettori sono ortogonali tra loro.
$$ \vec{a} =\frac{d \: \vec{ ω} }{ dt } \vec{r} + \vec{ω} (0 ) - \vec{r} ( \vec{ω} \vec{ω} ) $$
$$ \vec{a} = \frac{d \: \vec{ ω} }{ dt } \vec{r} - \vec{r} ( \vec{ω} \vec{ω} ) $$
$$ \vec{a} = \frac{d \: \vec{ ω} }{ dt } \vec{r} - \vec{r} \vec{ω^2} $$
La derivata della velocità angolare dω/dt è l'accelerazione angolare α
$$ \vec{a} = \frac{d \: \vec{ ω} }{ dt } \vec{r} - \vec{r} \vec{ω^2} $$
$$ \vec{a} = α \vec{r} - \vec{r} \vec{ω^2} $$
Dove aT=α x r e aN=-ω2
$$ \vec{a} = a_T + a_N $$
Si ritorna così all'accelerazione vettoriale come somma dell'accelerazione tangenziale e dell'accelerazione normale.
L'accelerazione angolare
L'accelerazione angolare è uguale alla derivata della velocità angolare. Si indica con la lettera alfa. $$ α = \frac{d \: ω}{dt} $$
Sapendo che la velocità angolare è uguale al rapporto tra la velocità e il raggio ωv/R
$$ α = \frac{d \: ω}{dt} = \frac{d \: \frac{v}{R}}{dt} = \frac{1}{R} \cdot \frac{d \: v}{dt} $$
e che la derivata della velocità è l'accelerazione tangenziale aT=dv/dt
posso riscrivere la formula dell'accelerazione angolare anche come il rapporto tra l'accelerazione tangenziale e il raggio.
$$ α = \frac{d \: ω}{dt} = \frac{a_T}{R} $$
Nota. L'accelerazione angolare non va confusa con l'accelerazione di velocità. L'accelerazione angolare misura l'accelerazione della velocità angolare mentre l'accelerazione di velocità misura la variazione della velocità del punto materiale sulla circonferenza.
Poiché la velocità angolare ω(t) è la derivata della legge oraria angolare θ(t), posso scrivere la formula dell'accelerazione angolare α(t) anche come derivata seconda della legge oraria angolare.
$$ α = \frac{d^2 \: θ}{dt^2} $$
Viceversa, conoscendo l'accelerazione angolare (α) posso risalire alla velocità angolare (ω) con una operazione di integrazione.
$$ \int_{t_0}^t α(t) \: dt = ω(t) + ω_0 $$
Una volta nota la velocità angolare (ω) posso risalire alla legge oraria angolare (θ) con un secondo integrale.
$$ \int_{t_0}^t ω(t) \: dt = θ(t) + θ_0 $$
Il moto circolare vario
Nel moto circolare varia la velocità è variabile in modulo e direzione.
Pertanto, l'accelerazione centripeta è sempre diversa da zero. In questo moto agiscono sia l'accelerazione centripeta (aN≠0) che l'accelerazione tangenziale (aT≠0).
Il centro della circonferenza varia in continuazione.
Nota. Un caso particolare di moto circolare vario è il moto circolare uniformemente accelerato dove la velocità è variabile (moto non uniforme) e l'accelerazione è una costante diversa da zero.
Il moto circolare uniforme
Nel moto circolare uniforme il modulo della velocità è costante, mentre varia in direzione e verso.
Pertanto, l'accelerazione tangente è nulla (aT=0).
In questo caso l'accelerazione coincide con l'accelerazione centripeta (a=aN).
Nel moto circolare uniforme v e ω sono costanti.
La legge oraria
La legge oraria del punto materiale è la seguente
$$ s(t) = s_0 + v \cdot t $$
Dove s0 è la posizione del punto nell'istante t=0.
La legge oraria dell'angolo è
$$ θ(t) = θ_0 + ω \cdot t $$
Dove θ0 è l'angolo nell'istante t=0.
Le coordinate del punto materiale nel moto circolare sono le seguenti:
$$ x(t) = R \cdot \cos θ(t) = R \cdot \cos (θ_0 + ω \cdot t) $$
$$ y(t) = R \cdot \sin θ(t) = R \cdot \sin (θ_0 + ω \cdot t) $$
E così via.
