Il segnale sinusoidale
Un segnale sinusoidale è un segnale periodico e regolare che si ripete in un periodo di tempo t $$ y= A \cdot \cos (ω_0 \cdot t + φ) $$
- A è l'ampiezza (picco)
- ω0 è la frequenza radiante
- φ è l'angolo di fase, ossia lo slittamento rispetto all'origine
- t è la variabile tempo
Nota. Il segnale sinusoidale può essere realizzato tramite le funzioni trigonometriche seno e coseno. Per convenzione si utilizza il coseno.
Ecco la rappresentazione base del segnale sinusoidale con A=1, φ=0 e ω0=1.
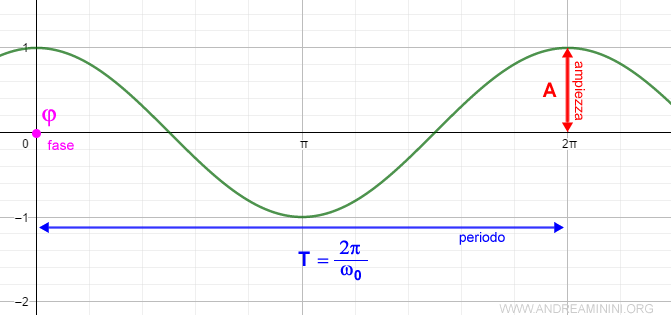
Il segnale sinusoidale si ripete regolarmente in un periodo di tempo T0
$$ T_0 = \frac{2π}{ω_0} $$
Il periodo è il reciproco della frequenza che si misura in cicli per secondo (o hertz).
$$ f_0 = \frac{1}{T_0} = \frac{ω_0}{2π} $$
Perché si studia il segnale sinusoidale? Il segnale sinusoidale caratterizza diversi fenomeni. Ad esempio, è l'onda tipica della corrente alternata v(t) nel dominio del tempo. $$ v(t) = A \cdot \cos (w_0 \cdot t + f ) $$
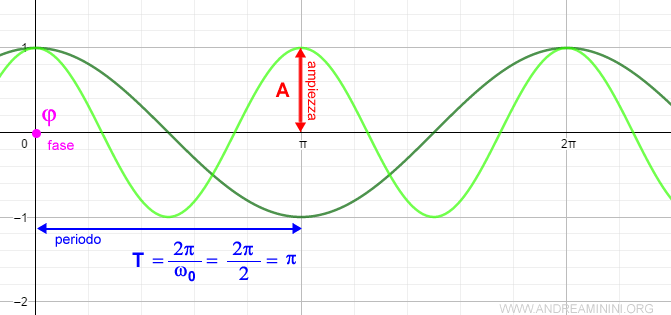
Pertanto, l'incremento della frequenza radiante ω0 riduce il periodo.
Ad esempio, se raddoppio la frequenza radiante a ω0 = 2 il periodo T del segnale precedente si accorcia da 2π a π
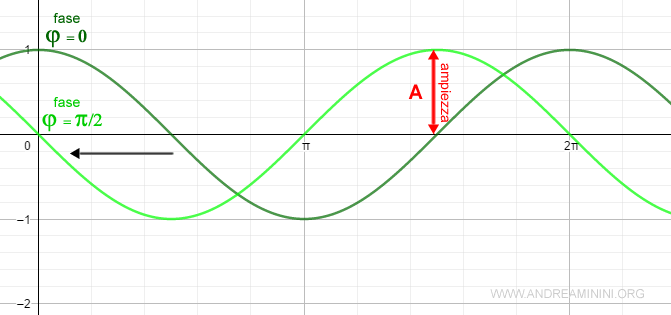
La variazione della fase φ, invece, effettua una traslazione del grafico rispetto all'origine.
Ad esempio, se aumento la fase da φ=0 a φ=π/2, il valore iniziale del coseno per t=0 passa da cos(0)=1 a cos(π/2)=0.
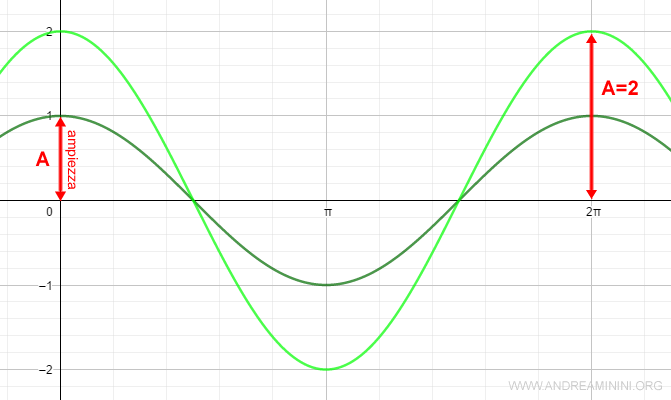
Infine, la variazione dell'ampiezza modifica l'altezza del picco.
Ad esempio, se modifico l'ampiezza da A=1 ad A=2 il grafico del segnale diventa
La rappresentazione della sinusoide sul piano complesso
La funzione sinusoidale può essere rappresentata come numero complesso esponenziale o fasore.
Cos'è il fasore? Il fasore è un numero complesso. E' utile per rappresentare le grandezze fisiche oscillanti come un vettore sul piano di Gauss.
Esempio
Prendo in considerazione la funzione periodica
$$ y = A \cdot \cos θ $$
L'angolo θ è equivalente a un numero complesso composto da una pulsazione ω0 e una fase φ.
La fase misura l'angolo φ nell'istante t=0.
$$ θ = ω_0 \cdot t + φ $$
Quindi, posso riscrivere la funzione periodica in questa forma.
$$ y = A \cdot \cos (ω_0 \cdot t + φ) $$
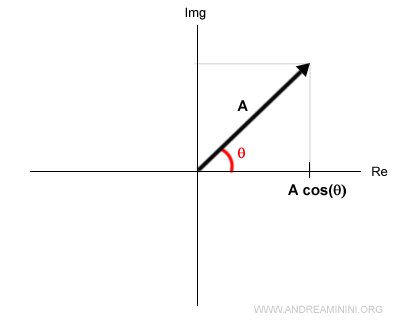
L'argomento del coseno θ è l'angolazione di un vettore rispetto all'asse reale del piano di Gauss.
Il modulo del vettore (ossia la lunghezza) è pari ad A.
Posso scrivere il segnale anche in forma esponenziale complessa poiché il coseno è la parte reale della formula di Eulero
$$ y = Re[ A \cdot e^{i(ω_0 \cdot t + φ)} ] $$
$$ y = Re [ A \cdot e^{iω_0t} e^{iφ} ] $$
Al variare del tempo il modulo A del vettore non cambia.
Quindi, nel corso del tempo (t) il vettore ruota tracciando una traiettoria circolare.
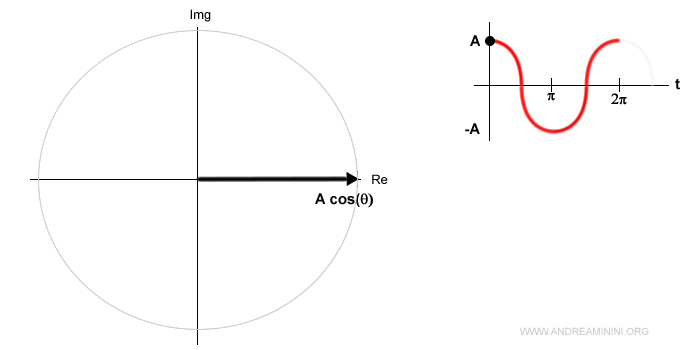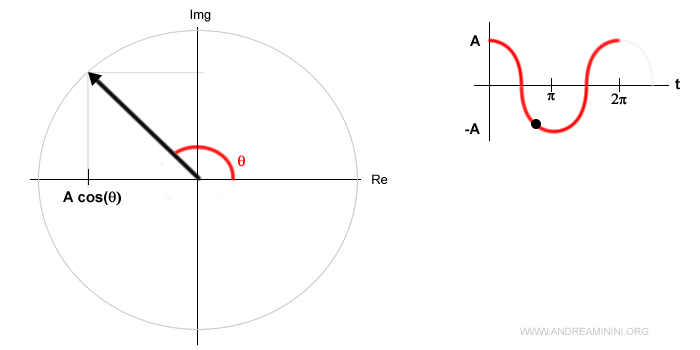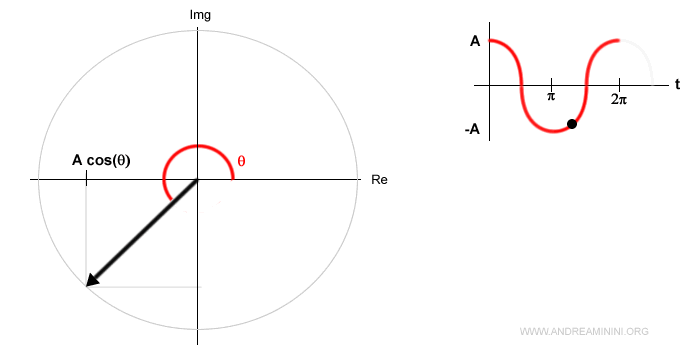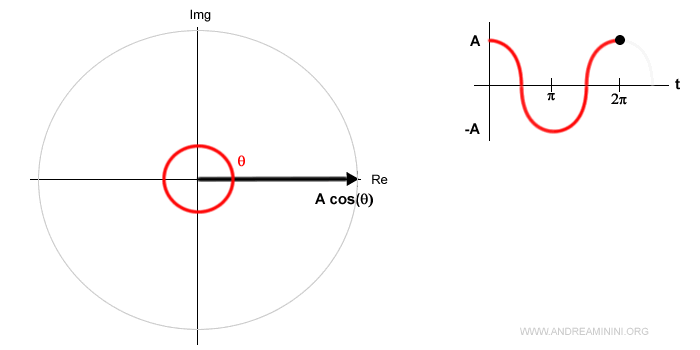
La proiezione del segnale sull'asse reale del piano di Gauss descrive il segnale sinusoidale A·cos(θ).
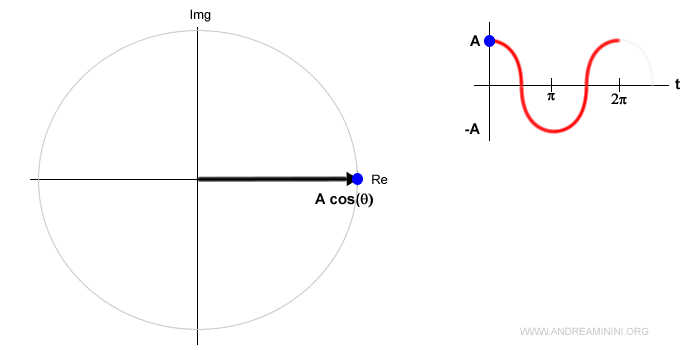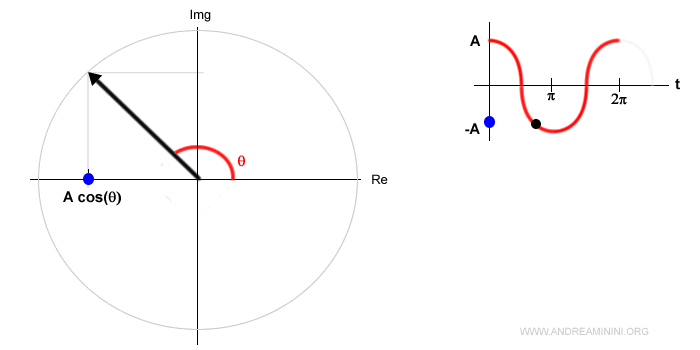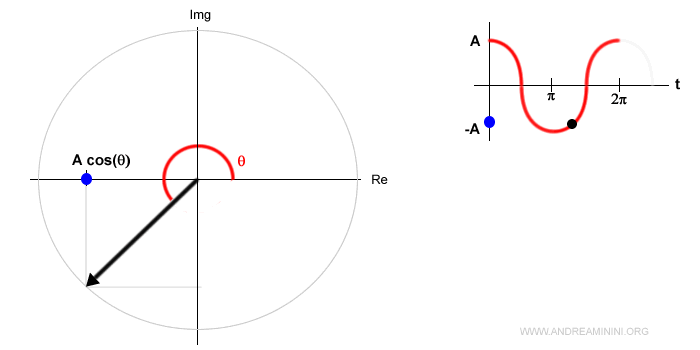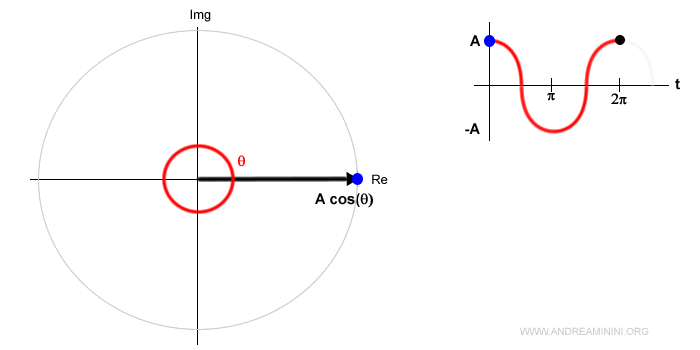
La fase invece descrive l'angolazione del vettore al momento iniziale.
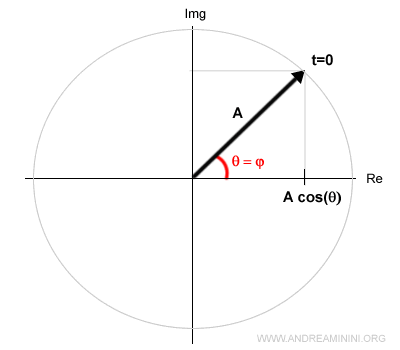
Nell'esempio precedente la fase è nulla φ=0. Quindi l'angolo iniziale è θ=0 rad.
Esempio. Se la fase fosse φ=π/4 nell'istante t=0 il vettore avrebbe un angolo iniziale di 45° ossia π/4.
Poiché ogni numero complesso z ha un numero coniugato z*, al fasore z corrisponde sempre un altro fasore coniugato z*
$$ z = A \cdot e^{if}e^{iw_0t} $$
$$ z* = A \cdot e^{-if}e^{-iw_0t} $$
C'è una stretta relazione tra i due fasori (z e z*) e la posizione sull'asse reale ossia il segnale
$$ \frac{z+z*}{2} = A \cos θ $$
Basta fare la media aritmetica dei due fasori.
$$ \frac{z+z*}{2} = \frac{ z \cdot e^{iφ}e^{iω_0t} + A \cdot e^{-iφ}e^{-iω_0t } }{2} $$
$$ \frac{z+z*}{2} = \frac{z}{2} \cdot e^{iφ}e^{iω_0t} + \frac{z}{2} \cdot e^{-iφ}e^{-iω_0t } $$
La somma di due vettori si effettua con la regola del parallelogramma
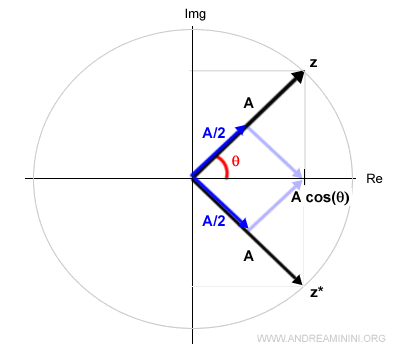
Quindi
$$ \frac{z+z*}{2} = A \cos θ = \frac{z}{2} \cdot e^{iφ}e^{iω_0t} + \frac{z}{2} \cdot e^{-iφ}e^{-iω_0t } $$
Questa relazione è molto utile nell'analisi dello spettro di frequenze.
E così via
