Moto armonico semplice
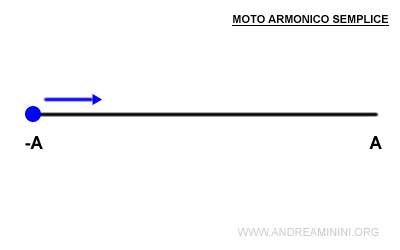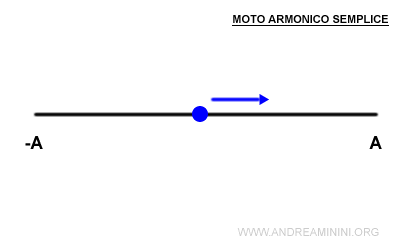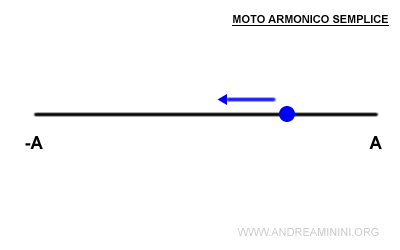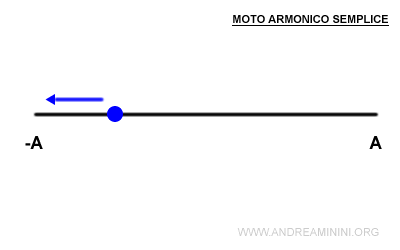
Il moto armonico semplice è un moto periodico lungo un asse rettilineo detto origine (O) che rispetta la seguente legge oraria $$ x(t)= A \cdot sin(ωt+φ) $$ Dove x(t) è la posizione, A è l'ampiezza, φ è la fase iniziale al tempo t=0, ω è la pulsazione, ωt+φ è la fase del moto con A, φ, ω grandezze costanti.
La velocità nel moto armonico semplice è una grandezza variabile $$ v(t) = ωA \: \cos(ωt+φ)$$ L'accelerazione è variabile ed è sempre opposta e proporzionale allo spostamento rispetto al centro dell'oscillazione. $$ a(t) = -ω^2 \: x(t) $$
Le principali variabili del moto sono l'ampiezza, l'origine, la fase, il periodo, la pulsazione che permettono di calcolare la frequenza, la velocità e l'accelerazione del moto armonico semplice.
Nota. Il moto armonico semplice descrive molti fenomeni oscillatori. Ad esempio, il moto del pendolo o di una molla.
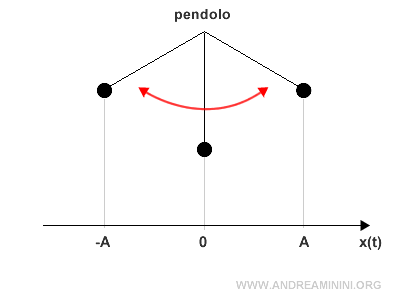
L'ampiezza del moto
La funzione trigonometrica seno ha un range di variazione da -1 a 1.
Pertanto, la funzione oraria x(t) varia da A a -A.
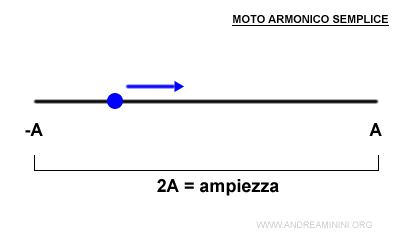
Quindi l'ampiezza del moto armonico è pari a 2A.
Lo spostamento massimo rispetto all'origine (O) dipende, invece dalla posizione dell'origine.
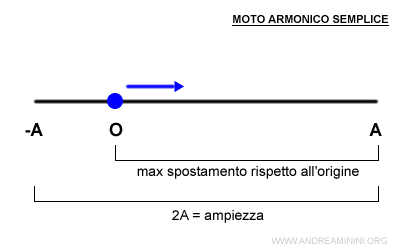
Se l'origine si trova in uno degli estremi lo spostamento massimo coincide con l'ampiezza.
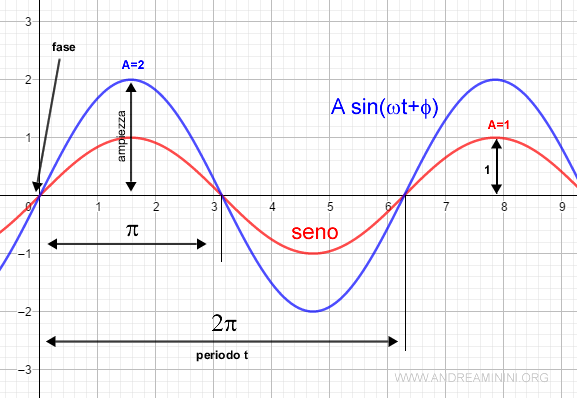
L'origine e la fase
L'origine (O) del moto armonico è la posizione del punto nell'istante iniziale.
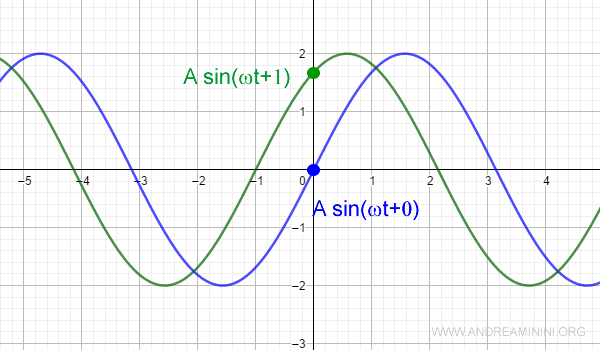
Nell'istante iniziale t=0 la funzione comincia il suo moto dal punto x(0) in base alla fase
$$ x(0) = A sin(φ) $$
Nota. Se indico un valore di fase diverso, il moto comincia da un punto diverso sull'asse delle ordinate. Soltanto se φ=0 l'origine (O) del moto coincide con l'origine degli assi cartesiani.
Il periodo
Il periodo T del moto armonico è 2π (360°) e indica la durata (o intervallo) di un'oscillazione completa rispetto al centro O.
Nell'intervallo di tempo T=t'-t la funzione x(t) ripassa nello stesso punto.
$$ x(t')=x(t) $$
Quindi
$$ ωt'+φ = ωt+φ+2π $$
Nota. Essendo un intervallo di tempo costante, il moto del punto è detto periodico.
Dalle precedenti si deduce che il periodo T=t'-t è uguale a
$$ T = \frac{2π}{ω} $$
Dimostrazione. $$ ωt'+φ = ωt+φ+2π \\ ωt'-ωt = φ+2π - φ \\ ω(t'-t) = 2π \\ t'-t = \frac{2π}{ω} \\ T = \frac{2π}{ω} $$
e la pulsazione ω è uguale a
$$ ω = \frac{2π}{T} $$
Dimostrazione. $$ ωt'+φ = ωt+φ+2π \\ ωt'-ωt = φ+2π - φ \\ ω(t'-t) = 2π \\ ω = \frac{2π}{t-t'} \\ ω = \frac{2π}{T} $$
La pulsazione
La pulsazione è la velocità angolare del moto ossia la velocità con cui varia l'angolo.
La pulsazione ω determina la lunghezza del periodo T.
- Se ω è alto il periodo T è basso
- Se ω è basso il periodo T è alto
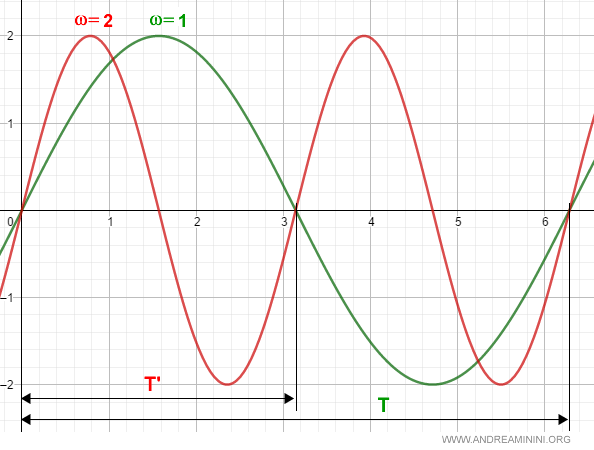
Nota. Ecco un esempio tra due pulsazioni ω=1 (verde) e ω=2 (rossa). Il segnale con ω=2 ha un periodo T' pari alla metà dell'altro periodo T perché la pulsazione è doppia rispetto a ω=1. E così via.
La frequenza
La frequenza v è il numero di oscillazioni in un secondo.
$$ v=\frac{1}{T}=\frac{ω}{2π} $$
La frequenza e il periodo dipendono dalle pulsazioni e sono indipendenti dall'ampiezza del moto e dalla fase.
La velocità del moto armonico
La velocità del moto armonico semplice è
$$ v(t) = ωA \: \cos(ωt+φ)$$
La velocità del moto armonico semplice non è costante.
- La velocità si riduce quando il corpo si allontana dal centro di oscillazione (origine O).
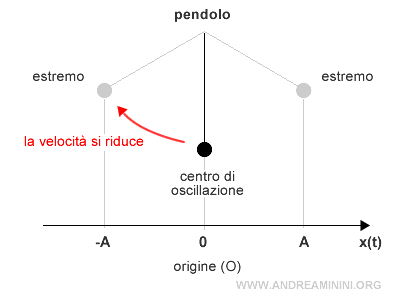
- La velocità si annulla del tutto v(t)=0 quando il moto raggiunge uno degli estremi dell'ampiezza x=A e x=-A.
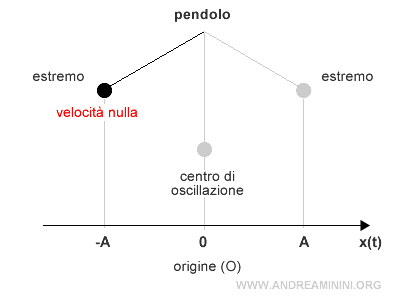
In questo punto si inverte il senso del moto $$ v(t) = 0 $$ - La velocità aumenta quando la velocità si muove verso il centro di oscillazione (origine O).
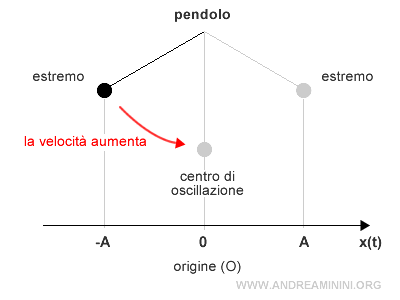
- La velocità è massima v(t)=ωA quando il moto passa per l'origine x=O.
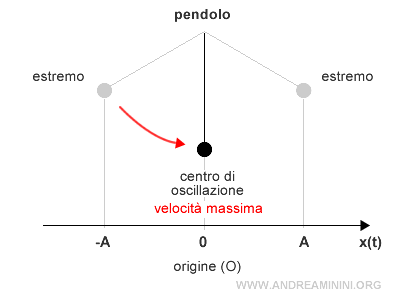
Nel punto O la velocità raggiunge il suo valore massimo $$ v(t) = ωA $$
Pertanto, il moto del pendolo decelera quando si allontana dall'origine e accelera quando si avvicina all'origine.
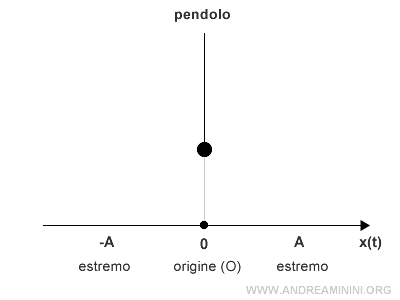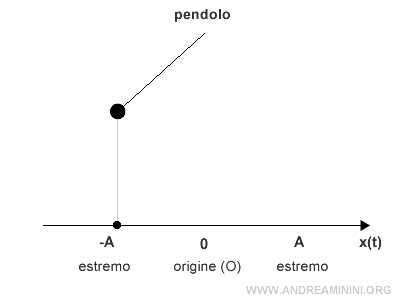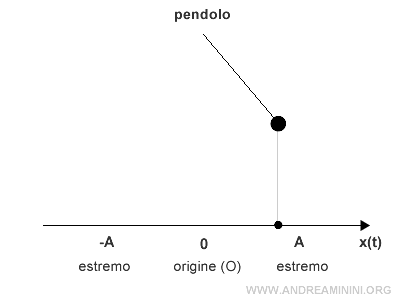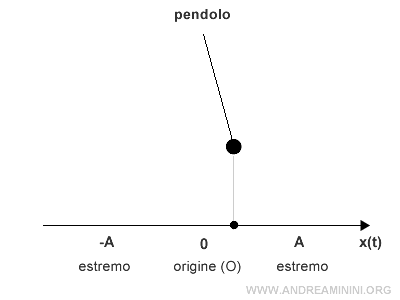
Nota. La relazione inversa tra la legge oraria x(t) e la velocità v(t) nel moto armonico semplice è evidente guardando il grafico delle sinusoidi.
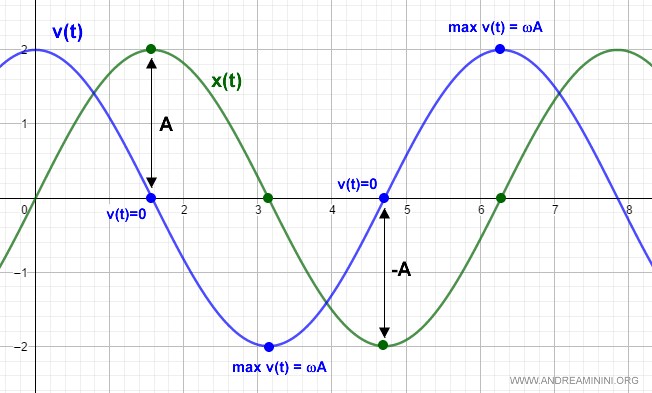
Il periodo e la frequenza della velocità è la stessa della legge oraria anche se sfasato nel tempo di π/2 (quadratura di fase). Soltanto l'ampiezza è diversa.
Dimostrazione
La velocità è la derivata prima della legge oraria x(t)
$$ v(t) = \frac{∂ x(t)}{∂t} $$
Sapendo che la legge oraria del moto armonico semplice è
$$ x(t)= A \: \sin(ωt+φ) $$
riscrivo la velocità in questo modo
$$ v(t) = \frac{∂ x(t)}{∂t} = D[A sin(ωt+φ)] $$
Poi calcolo la derivata prima
$$ v(t) = \frac{∂ x(t)}{∂t} = D[A sin(ωt+φ)] = ωA \: \cos(ωt+φ)$$
In questo modo ottengo la formula della velocità nel moto armonico semplice.
L'accelerazione del moto armonico
La formula dell'accelerazione nel moto armonico semplice è
$$ a(t) = -ω^2A \: \sin(ωt+φ) $$
Essendo la legge oraria
$$ x(t) = A \: \sin(ωt+φ) $$
Posso riscrivere la formula dell'accelerazione anche in forma più compatta
$$ a(t) = -ω^2 \: x(t) $$
L'accelerazione aumenta quando il corpo si sposta da un estremo verso il centro di oscillazione.
Viceversa, l'accelerazione si riduce quando il corpo si allontana dal centro di oscillazione.
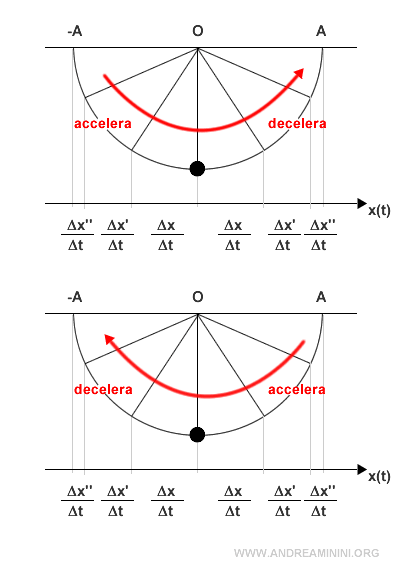
In conclusione, il modulo dell'accelerazione è massimo agli estremi quando si inverte il senso del moto (x=A e x=-A).
$$ a(t)=|-ω^2A| $$
L'accelerazione si annulla nel punto di origine O (x=0).
$$ a(t)=|-ω^2 \cdot 0 | = 0 $$
E' comunque proporzionale e opposta allo spostamento del punto x(t).
Nota. La relazione tra la legge oraria x(t) e l'accelerazione a(t) sul diagramma cartesiano.
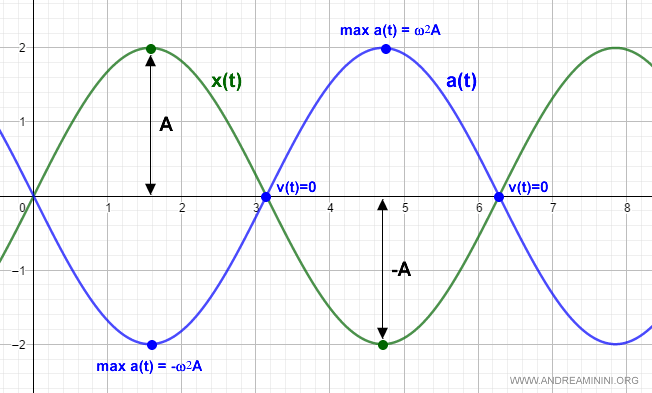
Il periodo e la frequenza dell'accelerazione è la stessa della legge oraria anche se sfasato nel tempo di π (opposizione di fase). Soltanto l'ampiezza è diversa.
Dimostrazione
In fisica l'accelerazione è la derivata della velocità.
$$ a(t) = \frac{∂ v(t)}{∂t} $$
Sapendo che la velocità nel moto armonico semplice è
$$ v(t) = ωA \: \cos(ωt+φ) $$
Riscrivo la formula dell'accelerazione in questo modo
$$ a(t) = \frac{∂ v(t)}{∂t} = D[ωA \: \cos(ωt+φ)] $$
Poi calcolo la derivata
$$ a(t) = \frac{∂ v(t)}{∂t} = D[ωA \: \cos(ωt+φ)] = -ω^2A \: \sin(ωt+φ) $$
Ho ottenuto la formula dell'accelerazione nel moto armonico semplice.
Nota. L'accelerazione è la derivata seconda del moto, essendo la velocità la derivata prima del moto. $$ a(t) = \frac{∂^2 x(t)}{∂t} = D^2[A \ sin(ωt+φ)] = -ω^2A \: \sin(ωt+φ) $$ Quindi, l'accelerazione dipende dalla legge del moto x(t) ossia dalla posizione del corpo durante il moto. $$ a(t) = \frac{∂^2 x(t)}{∂t^2} $$ Sapendo che la formula dell'accelerazione è -ωx(t), si tratta di trovare la soluzione alla sequente equazione differenziale $$ \frac{∂^2 x(t)}{∂t^2} = -ω^2 \cdot x(t) $$ la cui soluzione è $$ x(t) = A \cdot \sin (ωt+φ) $$
Come calcolare la velocità dalla posizione
La formula per calcolare la velocità del moto armonico semplice dalla posizione del punto è
$$ v^2 = ω^2 (x_0^2 - x^2) + v_0^2 $$ o nel caso in cui il moto armonica parta da x0=0 $$ v^2 = ω^2 (A^2 - x^2) $$
Dimostrazione
Sapendo che tra lo spostamento nello spazio e la velocità c'è la seguente relazione:
$$ \int_{x_0}^{x} a(x) dx = \int_{v_0}^{v} v \: dv $$
e che nel moto orario l'accelerazione è -ω^2x
$$ \int_{x_0}^{x} -ω^2x \: dx = \int_{v_0}^{v} v \: dv $$
svolgo tutti i calcoli
$$ -ω^2 \int_{x_0}^{x} x dx = \frac{1}{2}v^2 - \frac{1}{2} v_0^2 $$
$$ -ω^2 ( \frac{1}{2}(x^2 - x_0^2) ) = \frac{1}{2}v^2 - \frac{1}{2} v_0^2 $$
$$ ω^2 ( \frac{1}{2}(x_0^2 - x^2) ) = \frac{1}{2}v^2 - \frac{1}{2} v_0^2 $$
$$ \frac{1}{2} ω^2 x_0^2 - \frac{1}{2} ω^2 x^2 = \frac{1}{2}v^2 - \frac{1}{2} v_0^2 $$
$$ \frac{1}{2} ω^2 x_0^2 - \frac{1}{2} ω^2 x^2 + \frac{1}{2} v_0^2 = \frac{1}{2}v^2 $$
$$ ω^2 x_0^2 - ω^2 x^2 + v_0^2 = v^2 $$
$$ ω^2 (x_0^2 - x^2) + v_0^2 = v^2 $$
Ho così ottenuto la formula iniziale.
$$ v^2 = ω^2 (x_0^2 - x^2) + v_0^2 $$
Partendo da x0=0 so già che la velocità armonica e v0=ωA
$$ v^2 = ω^2 (0^2 - x^2) + (ωA)^2 $$
$$ v^2 = - ω^2 x^2 + ω^2A^2 $$
$$ v^2 = ω^2 (A- x^2) $$
Ho così trovato la formula nel caso in cui il moto parta da x0=0.
L'equazione differenziale del moto armonico
L'equazione differenziale del moto armonico è $$ \frac{d^2 x(t)}{d^2 t} + w^2x = 0 $$
Dimostrazione
La legge oraria del moto armonico semplice è
$$ x(t) = A \sin(wt+f) $$
L'accelerazione è la derivata seconda della legge oraria:
$$ a(t) = D^2[x(t)] = \frac{d^2 x(t)}{d^2 t} $$
Sapendo che l'accelerazione del moto armonico semplice è
$$ a=-w^2x $$
Posso scrivere
$$ \frac{d^2 x(t)}{d^2 t} = -w^2x $$
Con un semplice passaggio algebrico ottengo l'equazione differenziale del moto armonico
$$ \frac{d^2 x(t)}{d^2 t} + w^2x = 0 $$
E così via.
