Analisi di un segnale con la serie di Fourier
Un segnale periodico v(t) in un periodo T0=1/f0 può essere scomposto in somme di sinusoidi o di fasori rosanti tramite la serie esponenziale di Fourier. $$ v(t) = \sum_{n=-∞}^{∞} c_n \cdot e^{j2πnf_0t} $$
La spiegazione
I coefficienti cn della serie di Fourier e sono uguali alla media del prodotto v(t)e-j2πnf0t mentre j è l'unità immaginaria i=√-1 del numero complesso.
$$ c_n = \frac{1}{T_0} \int_{T_0} v(t)e^{-j2πnf_0t} \: dt $$
La variabile n=0,1,2,.... indica i cicli del periodo 2π.
La variabile f0 è la frequenza ed è pari all'inverso del periodo f0=1/T0.
Nota. In matematica la serie di Fourier mi permette di rappresentare una funzione periodica mediante una combinazione lineare di funzioni sinusoidali (seno e coseno). $$ f(x) = a_0 + \sum_{k=1}^{\infty} (a_k \cos k \cdot x + b_k \sin k \cdot x ) $$ I parametri a0, ak e bk sono detti coefficienti di Fourier. Usando la formula di Eulero $$ e^{jθ} = \cos θ + i \cdot \sin θ $$ dove è l'unità immaginaria i=√-1 e θ è un angolo qualsiasi, posso riformulare la serie di Fourier in modo equivalente nella forma esponenziale $$ v(t) = \sum_{n=-∞}^{∞} c_n e^{j2πnf_0t} $$
Se il coefficiente cn è un numero complesso posso rappresentarlo anche in forma polare.
$$ c_n = |c_n| = e^{j(arg \: c_n)} $$
dove |cn| è il modulo (ampiezza) e arg cn è l'argomento (l'angolo) di cn.
Il modulo |c(nf0)| rappresenta lo spettro delle frequenze.
L'argomento arg c(nf0) rappresenta lo spettro della fase.
Settando n=0 il coefficiente c(0) è pari al valore medio del segnale $$ c(0)= \frac{1}{T_0} \int_{T_0} v(t) \: dt = <v(t)> $$
Se la funzione del segnale nel dominio del tempo v(t) non è un numero complesso, ossia è una funzione reale, lo spettro dell'ampiezza e della fase sono simmetrici rispetto all'asse delle ordinate
$$ |c_{nf_0}|= |-c_{nf_0}| $$ $$ arg \: c(-nf_0) = -arg \: c(nf_0) $$
Lo spettro dell'ampiezza ha simmetria pari mentre lo spettro della fase ha simmetria dispari.
Esempio
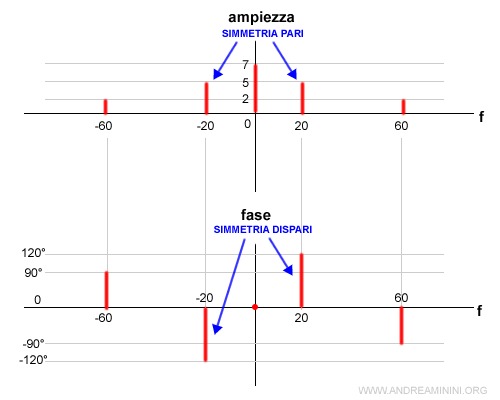
Nel caso dei segnali reali la serie di Fourier esponenziale può essere riscritta sotto forma di serie di Fourier trigonometrica tramite coppie complesse e coniugate.
$$ v(t) = c_0 + \sum_{n=1}^{∞} |2c_n| \cos (2πnf_0t + \: arg \: c_n) $$
La precedente formula disegna soltanto una parte del diagramma e non entrambe.
Spesso l'integrale del coefficiente cn comporta un fasore in media
$$ c_n = \int_{-T/2}^{T/2} e^{-j2πft} \: dt = \frac{1}{j2πfT}(e^{jπfT} - e^{-jπfT}) = \frac{1}{πfT} \frac{e^{jπfT} - e^{-jπfT}}{2j} $$
Sapendo che secondo la formula di Eulero il seno è uguale alla differenza di esponenziali complessi
$$ \sin z = \frac{e^{jz}-e^{-jz}}{2j} $$
assegnando z=πfT ottengo la forma equivalente
$$ c_n = \frac{1}{πfT} \sin πfT $$
Per semplicità introduco la funzione del seno cardinale (sinc)
$$ sinc \: A = \frac{\sin πλ}{πλ} $$
Assegnando λ=fT posso trasformare il coefficiente cn della serie Fourier in questa forma ridotta e semplificata dove A è la variabile indipendente.
$$ c_n = \frac{1}{πfT} \: sinc \: A $$
Un esempio pratico
Un segnale periodico è composto da impulsi rettangolari. Ad esempio, un segnale di clock in un computer.
Per semplicità l'ampiezza dell'impulso è A=1 e la durata è τ=2T1.
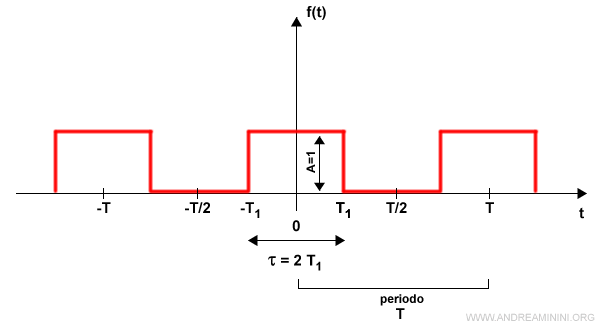
L'onda rettangolare ha un periodo (durata) pari a T.
Per determinare i coefficienti di Fourier considero l'intervallo di tempo
$$ - \frac{T}{2} \le t \le \frac{T}{2} $$
Quindi, nel dominio del tempo la funzione si può scrivere
$$ f(t) =\begin{cases} 1 \:\: se \:\: |t| < T_1 \\ \\ 0 \:\: se \:\: T_1 < |t| < T/2 \end{cases} $$
La frequenza del segnale ω è
$$ ω_0 = \frac{2π}{T} $$
Per n = 0 il coefficiente c0 è
$$ c_0 = \frac{1}{T} \int_{-T_1}^{T_1} \: dt $$
$$ c_0 = \frac{1}{T} \cdot [ t ]_{-T_1}^{T_1} $$
$$ c_0 = \frac{1}{T} \cdot [ T_1 -(-T_1) ] $$
$$ c_0 = \frac{2T_1}{T} $$
Per n>0 i coefficienti cn sono
$$ c_n = \frac{1}{T} \int_{-T_1}^{T_1} e^{-jnω_0t} \: dt = \frac{2T_1}{T} $$
Applico la regola fondamentale di integrazione
$$ c_n = \frac{1}{T} [ - \frac{1}{jnω_0} e^{-jnω_0t} ]_{-T_1}^{T_1} $$
$$ c_n = \frac{1}{T} [ - \frac{1}{jnω_0} e^{-jnω_0T_1} - (- \frac{1}{inω_0} e^{-jnω_0(-T_1)}) ] $$
$$ c_n = \frac{1}{T} [ - \frac{1}{jnω_0} e^{-jnω_0T_1} + \frac{1}{inω_0} e^{jnω_0T_1}) ] $$
$$ c_n = \frac{1}{T} [ \frac{1}{jnω_0} e^{jnω_0T_1} - \frac{1}{inω_0} e^{-jnω_0T_1} ] $$
$$ c_n = \frac{1}{jnω_0T} \cdot [ e^{jnω_0T_1} - e^{-jnω_0T_1} ] $$
$$ c_n = \frac{1}{jnω_0T} \cdot [ e^{jnω_0T_1} - e^{-jnω_0T_1} ] $$
$$ c_n = \frac{1}{nω_0T} \cdot [ \frac{e^{jnω_0T_1} - e^{-jnω_0T_1}}{j} ] $$
Nota. Sapendo che secondo il seno è uguale alla differenza di esponenziali complessi $$ \sin z = \frac{e^{jz}-e^{-jz}}{2j} $$ allora $$ 2 \sin z = \frac{e^{jz}-e^{-jz}}{j} $$ dove z=nωT1
$$ c_n = \frac{1}{nω_0T} \cdot [ 2 \sin(nω_0T_1) ] $$
$$ c_n = \frac{2 \sin(nω_0T_1)}{nω_0T} $$
Essendo ω0T=2π
$$ c_n = \frac{2 \sin(nω_0T_1)}{n(2π)} $$
$$ c_n = \frac{\sin(nω_0T_1)}{nπ} $$
Questa formula con n=1,2,3,... mi permette di calcolare gli altri coefficienti di Fourier c1, c2,c3,...
Una volta ottenuti i coefficienti posso disegnare lo spettro di frequenza del segnale.
Cos'è lo spettro di frequenza? Ogni segnale periodico è caratterizzato da uno spettro di frequenza in cui si associa l'ampiezza e la fase del segnale per ogni frequenza.
Il coefficiente cn può essere scritto nella forma
$$ c_n = |c_n| e^{jθ_n} $$
Dove |cn| è il modulo o ampiezza mentre θn è la fase.
Per disegnare lo spettro delle frequenze utilizzo il seno cardinale $$ sinc(x) = \frac{\sin(x)}{x} $$ La fase è nulla per i valori positivi della funzione sinc() e π (o -π) per i valori negativi.
Riprendo la formula del coefficiente cn
$$ c_n = \frac{2 \sin(nω_0T_1)}{nω_0T} $$
Per applicare la funzione sinc() devo fare in modo che l'argomento del seno sia uguale al denominatore.
Quindi, moltiplico e divido per T1.
$$ c_n = \frac{2 \sin(nω_0T_1)}{nω_0T} \cdot \frac{T_1}{T_1} $$
$$ c_n = 2 \cdot \frac{ \sin(nω_0T_1)}{nω_0T_1} \cdot \frac{T_1}{T} $$
$$ c_n = 2 \cdot \: sinc (nω_0T_1) \cdot \frac{T_1}{T} $$
$$ c_n = \frac{2T_1}{T} \cdot \: sinc (nω_0T_1) $$
Per semplificare ulteriormente la formula sostituisco ω=nω0
$$ c_n = \frac{2T_1}{T} \cdot \: sinc (ωT_1) $$
A questo punto posso calcolare le armoniche nelle varie frequenze.
Per ω=0
Quando ω=0 il seno cardinale vale 1.
$$ sinc(0) = 1 $$
Quindi, l'ampiezza in c0 è
$$ |c_n| = | \frac{2T_1}{T} \cdot \: sinc(0) | $$
$$ |c_n| = \frac{2T_1}{T} \cdot 1 $$
$$ |c_n| = \frac{2T_1}{T} $$
Nota. L'ampiezza in c0 è uguale al valore medio del segnale nel periodo T.
La funzione sinc() ha valore positivo sinc()=1>0, quindi la fase è nulla.
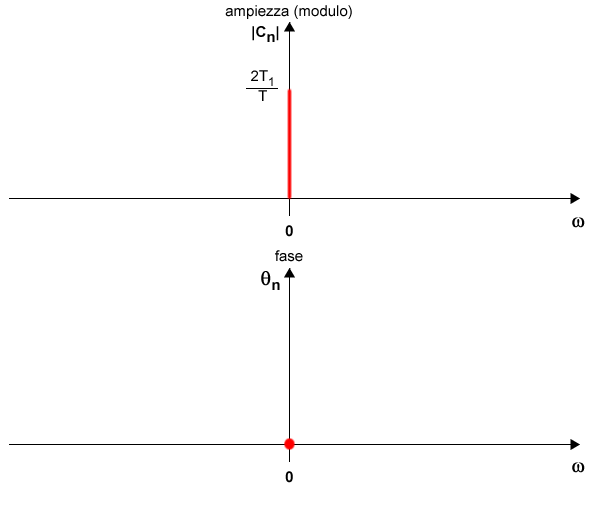
Da ω>0 a ω<π/T1
Nell'intervallo delle pulsazioni compreso tra ω∈(0,π/T1) il seno cardinale è positivo ed è compreso tra 0 e 1 .
$$ 0 < sinc(ωT_1) < 1 $$
Quindi, l'ampiezza del segnale è
$$ |c_n| = | \frac{2T_1}{T} \cdot \: sinc(ωT_1) | $$
$$ |c_n| = \frac{2T_1}{T} \cdot \: sinc(ωT_1) $$
Essendo la funzione sinc()>0 la fase è nulla nell'intervallo ω∈(0,π/T1)
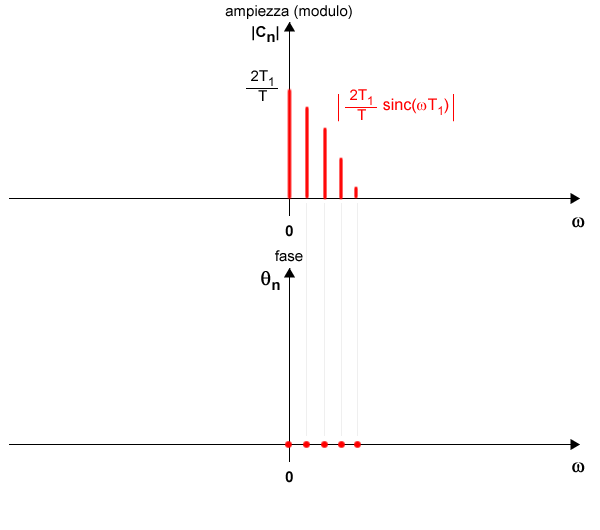
Per ω=π/T1
Alla frequenza ω=π/T1 il seno cardinale si annulla
$$ sinc(ωT_1) = sinc(\frac{π}{T_1}T_1) = sinc(π) = 0 $$
Pertanto, l'ampiezza (modulo) è uguale a zero
$$ |c_n| = | \frac{2T_1}{T} \cdot \: sinc(ωT_1) | $$
$$ |c_n| = | \frac{2T_1}{T} \cdot \: 0 | $$
$$ |c_n| = 0 $$
Non essendo positiva l'ampiezza, la fase è uguale a ±π ossia ±180°.
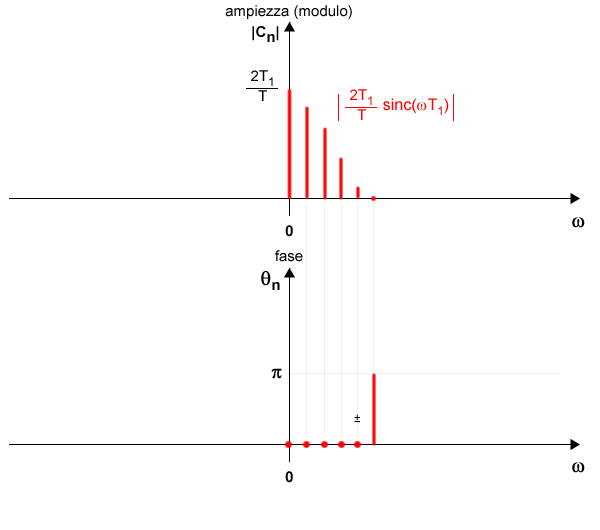
Da ω=π/T1 a ω=2π/T1
Nell'intervallo di frequenze ω=[π/T1,π/T1] il seno cardinale è negativo (non positivo). Quindi la fase è 180°.
L'ampiezza (modulo) è sempre positiva perché è sotto modulo. E' però inferiore rispetto al primo ciclo perché il valore del seno cardinale ora è più basso.
$$ |c_n| = | \frac{2T_1}{T} \cdot \: sinc(ωT_1) | > 0 $$
Ecco lo spettro aggiornato con le nuove frequenze
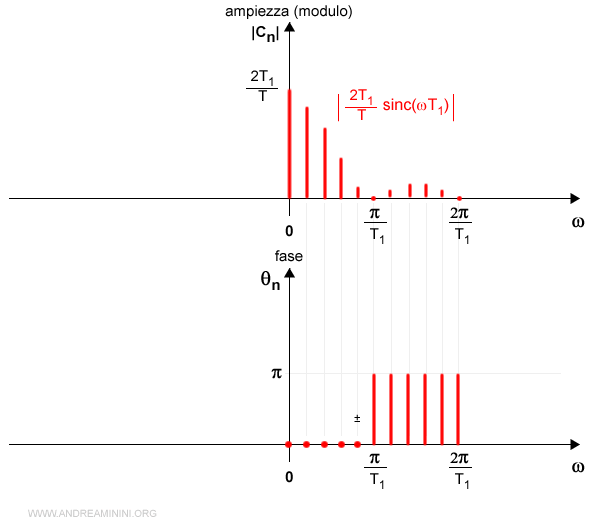
Per ω>2π/T1
Nell'intervallo di frequenze ω=[π/T1,π/T1] il seno cardinale torna a essere positivo. Quindi la fase è nulla.
L'ampiezza (modulo) è positiva ma inferiore rispetto ai cicli precedenti perché il valore del seno cardinale ora è ancora più basso.
$$ |c_n| = | \frac{2T_1}{T} \cdot \: sinc(ωT_1) | > 0 $$
Ecco lo spettro aggiornato con le nuove frequenze.
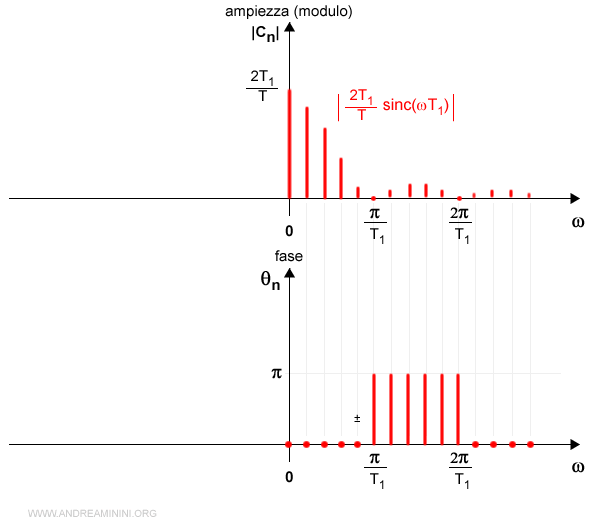
E così via.
