Punti notevoli del triangolo

I punti notevoli di un triangolo sono punti in cui si intersecano rette o segmenti particolari, come gli assi, le altezze, le mediane, ecc.

A cosa servono? Sono punti che hanno particolari proprietà geometriche. La conoscenza di questi punti e delle loro proprietà può facilitare la risoluzione di molti problemi geometrici legati ai triangoli.

Ecco alcuni dei più importanti:

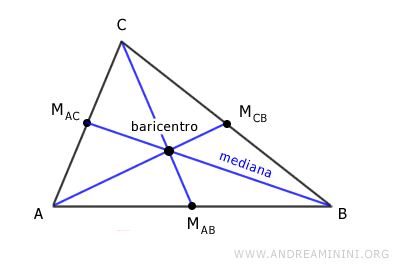
Baricentro

È il punto di incontro delle mediane di un triangolo. Una mediana è un segmento che unisce un vertice al punto medio del lato opposto. Il baricentro divide ogni mediana in due segmenti secondo il rapporto 2:1, con la porzione più grande vicino al vertice.

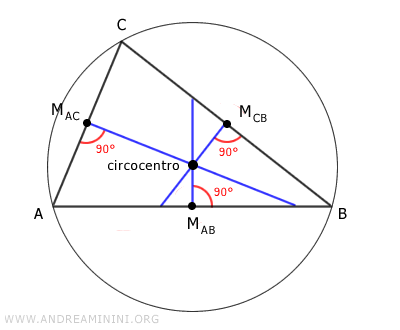
Circocentro

È il centro della circonferenza circoscritta al triangolo, detta anche circocerchio. Il circocentro è il punto di incontro delle perpendicolari (ortocentri) tracciate dal punto medio di ciascun lato del triangolo. La sua distanza da ciascun vertice è chiamata raggio circoscritto.

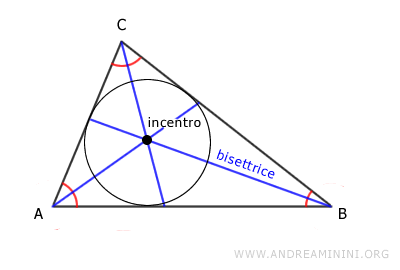
Incentro

È il centro della circonferenza inscritta nel triangolo, o incerchio. L'incentro è il punto di incontro delle bisettrici degli angoli interni del triangolo. La distanza dall'incentro a un lato del triangolo è chiamata raggio inscritto.

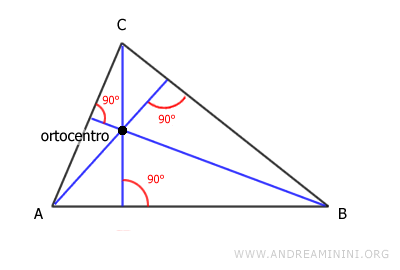
Ortocentro

È il punto di incontro delle altezze del triangolo. Un'altezza è un segmento perpendicolare tracciato da un vertice al lato opposto (o al suo prolungamento).

Excentro

Per ciascun angolo acuto di un triangolo, esiste un excentro, che è il centro di una circonferenza esterna tangente a un lato del triangolo e alle prolunghe degli altri due lati. Il triangolo ha tre excentri se è acuto o rettangolo e ne ha solo uno se è ottuso.

Punto di Fermat

È un punto tale che la somma delle distanze dai tre vertici del triangolo è minimizzata. È noto anche per i triangoli di Fermat, che sono triangoli equilateri tracciati esternamente ai lati di un altro triangolo, aventi il punto di Fermat come vertice opposto.

Punto di Brocard

In ogni triangolo, esistono due punti di Brocard, ognuno dei quali forma angoli di uguale misura con i lati del triangolo.

Punto di Nagel

È il punto di incontro delle linee che congiungono i punti di contatto dell'incerchio con i lati del triangolo e gli opposti vertici.

E così via.