Angoli associati in geometria

In geometria gli angoli sono detti "angoli associati" se sono legati tra loro da una relazione.

Gli angoli possono essere associati per ampiezza, per posizione o rispetto a due rette tagliate trasversalmente.

Angoli associati per ampiezza

Due angoli sono associati per ampiezza se la loro somma è un angolo retto oppure un multiplo dell'angolo retto.

In particolar modo, gli angoli associati per ampiezza sono detti:

• Angoli complementari
  Due angoli sono complementari se la loro somma è un angolo retto (90° o π/2 radianti).
  
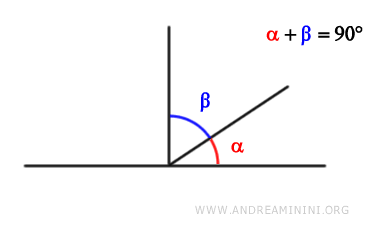
• Angoli supplementari
  Due angoli sono supplementari se la loro somma è un angolo piatto (180° o π radianti).
  
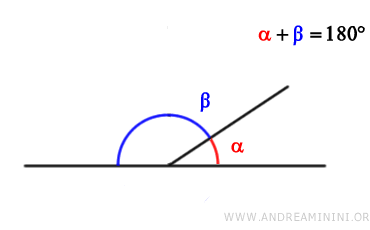
• Angoli esplementari
  Due angoli sono esplementari se la loro somma è un angolo giro (360° o 2π radianti).
  

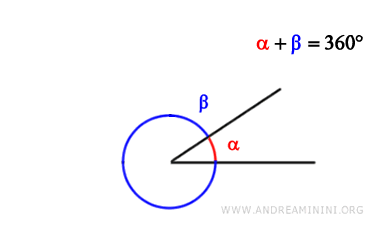
Angoli associati per posizione

Due angoli sono associati per posizione se hanno in comune uno o più lati, o i loro prolungamenti.

Esistono diversi angoli associati per posizione

• Angoli consecutivi
  Due angoli sono detti angoli consecutivi se hanno il vertice e un lato in comune.
  
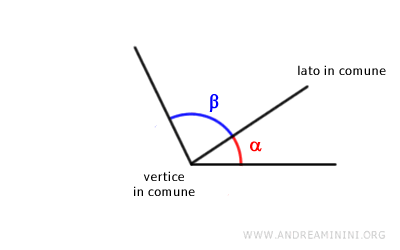
• Angoli adiacenti
  Due angoli sono detti angoli adiacenti se hanno in comune il vertice e un lato, mentre i lati non in comune sono sulla stessa retta.
  

  Nota. In altre parole, gli angoli adiacenti sono angoli consecutivi con i lati non in comune che giacciono sulla stessa retta. Due angoli adiacenti sono anche angoli supplementari, perché la loro somma è sempre uguale a un angolo piatto (180°).

• Angoli opposti al vertice
  Due angoli sono opposti al vertice se sono angoli non consecutivi, hanno il vertice in comune e i lati di un angolo sono il prolungamento dei lati dell'altro angolo.
  
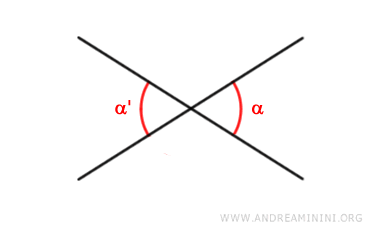
  Ad esempio, gli angoli α e α' sono angoli opposti al vertice.
  

  Nota. Due angoli opposti al vertice sono sempre congruenti perché hanno la stessa ampiezza.

Angoli associati rispetto a due rette tagliate trasversalmente

Se considero due rette "r" e "s" e le taglio in modo trasversale da un'altra retta "t", ottengo otto angoli legati tra loro da particolari relazioni.

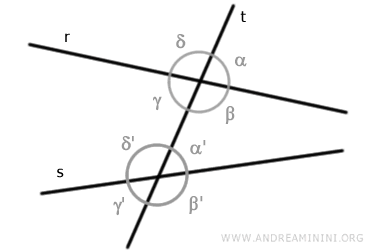
In questo caso le relazioni tra gli angoli associati sono le seguenti:

• Angoli alterni
  Sono le coppie di angoli che non hanno vertici in comune e appartengono a semipiani opposti rispetto alla retta "t".

  Sono detti alterni interni o alterni esterni a seconda se si trovano tra le due rette "r" e "s" oppure no. Ad esempio, le coppie di angoli (γ,α') e (β,δ') sono alterni interni.
  
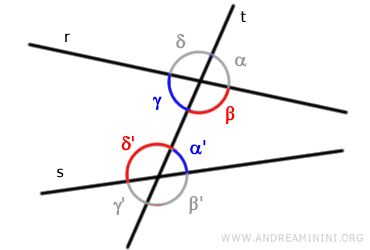
  Le coppie di angoli (α,γ') e (δ,β') invece sono alterni esterni.
  

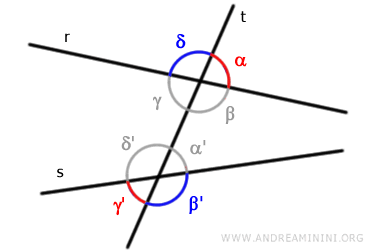
• Angoli coniugati
  Sono le coppie di angoli che non hanno vertici in comune e appartengono allo stesso semipiano rispetto alla retta "t".

  Sono detti coniugati interni o coniugati esterni se si trovano tra le due rette "r" e "s" oppure no. Ad esempio, le coppie di angoli (β,α') e (γ,δ') sono coniugati interni.
  
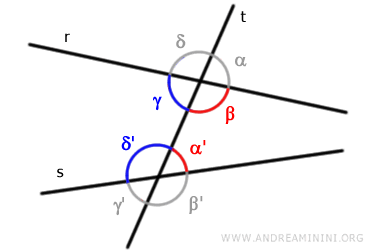
  Viceversa, le coppie di angoli (α,β') e (δ,γ') sono coniugati esterni.
  
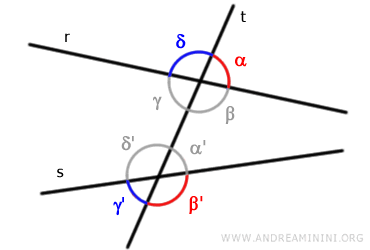
  Se le rette "r" e "s" sono parallele, gli angoli coniugati sono anche angoli supplementari perché hanno un'ampiezza uguale a un angolo piatto (180°).

• Angoli corrispondenti
  Sono le coppie di angoli che non hanno vertici in comune, appartengono allo stesso semipiano rispetto alla retta "t" e sono disposti uno all'interno e l'altro all'esterno.

  Ad esempio, sono angoli corrispondenti le coppie di angoli (α,α'), (β,β'), (γ,γ'), (δ,δ').
  
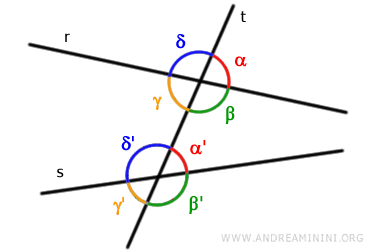
  Due angoli corrispondenti hanno la stessa ampiezza se e solo se le rette "r" e "s" sono parallele.

Angoli associati in trigonometria

In goniometria le coppie di angoli sono dette "angoli associati" se sono legati da particolari relazioni tramite le funzioni trigonometriche.

Ecco le principali relazioni goniometriche.

$$ \sin (- \alpha) = - \sin ( \alpha ) $$

$$ \sin ( \frac{ \pi }{2} - \alpha) = \cos ( \alpha ) $$

$$ \sin ( \frac{ \pi }{2} + \alpha) = \cos ( \alpha ) $$

$$ \sin ( \pi - \alpha) = \sin ( \alpha ) $$

$$ \cos ( - \alpha) = \cos ( \alpha ) $$

$$ \cos ( \frac{ \pi }{2} - \alpha) = \sin ( \alpha ) $$

$$ \cos ( \frac{ \pi }{2} + \alpha) = - \sin ( \alpha ) $$

$$ \cos ( \pi - \alpha) = - \cos ( \alpha ) $$

$$ \tan ( - \alpha) = - \tan ( \alpha ) $$

$$ \tan ( \frac{ \pi }{2} - \alpha ) =\cot ( \alpha ) $$

$$ \tan ( \frac{ \pi }{2} + \alpha ) = - \cot ( \alpha ) $$

$$ \tan ( \pi - \alpha) = - \tan ( \alpha ) $$

E così via.