L'addizione di angoli
Per sommare due angoli consecutivi basta calcolare l'ampiezza tra i due lati non comuni. $$ a \hat{O} b + b \hat{O} c = a \hat{O} c $$
Quando si parla di somma di angoli, si intende la somma delle ampiezze degli angoli, misurate in gradi o in radianti.
Esempio. Considero due angoli contigui aȮb e bȮc. I lati non in comune sono i lati a e c.
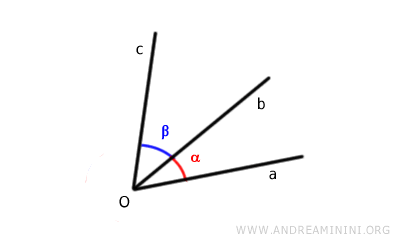
Quindi, per conoscere la somma degli angoli, basta misurare l'ampiezza dell'angolo tra i lati non in comune ossia aȮc.
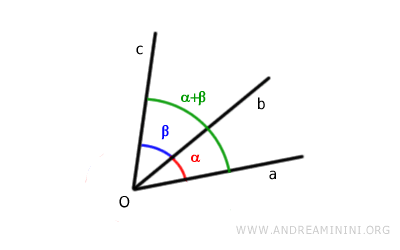
E come sommare gli angoli non consecutivi?
Dal punto di vista geometrico l'addizione tra gli angoli contigui può essere estesa anche agli angoli non contigui.
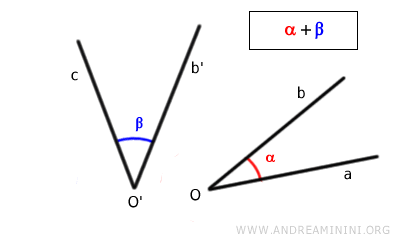
Ad esempio, considero due angoli non contigui.
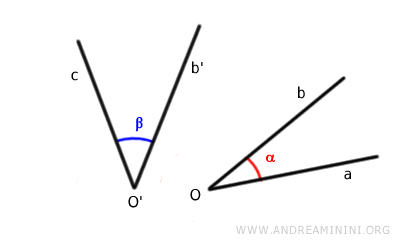
Sovrappongo il vertice del primo angolo al vertice del secondo angolo.
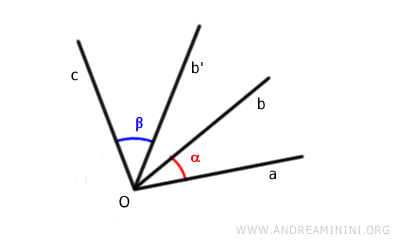
Con un movimento rigido sovrappongo un lato del primo angolo a un lato dell'altro angolo.

Ora i due angoli sono contigui e sono congruenti a quelli iniziali.
Quindi, posso applicare la stessa regola dell'addizione degli angoli contigui. In altre parole, misuro l'ampiezza tra i lati non in comune.

Nota. Dal punto di vista matematico, invece, basta misurare l'ampiezza dei due angoli α e β tramite un goniometro e sommare le ampiezze tra loro (α+β) indipendentemente dal fatto che gli angoli siano contigui o meno.
Le proprietà dell'addizione tra angoli
Alcune proprietà dell'addizione tra due o più angoli
- Dati due coppie di angoli congruenti α≅β e γ≅δ, allora anche la somma degli angoli α+γ=β+δ è congruente, ossia ha la stessa ampiezza. $$ \alpha \cong \beta \ , \ \gamma \cong \delta \ , \ \Longrightarrow \alpha + \gamma \cong \beta + \delta $$
- Dati quattro angoli, presi a coppie non congruenti, se α>β e γ>δ, allora anche la somma degli angoli α+γ>β+δ non è congruente e soddisfa la stessa relazione di ordine. $$ \alpha > \beta \ , \ \gamma > \delta \ , \ \Longrightarrow \alpha + \gamma > \beta + \delta $$
E così via.
