Postulato di Eudosso-Archimede sugli angoli

Secondo il postulato di Eudosso-Archimede, dati due angoli non congruenti e di ampiezza non nulla, è sempre possibile trovare un multiplo dell'angolo minore che supera l'angolo maggiore.

Questo è un importante principio nell'ambito della geometria euclidea.

Il postulato prende il nome dai matematici antichi Eudosso e Archimede che lo hanno proposto e utilizzato.

Nota. Si tratta dell'applicazione agli angoli del noto postulato di Eudosso-Archimede sui segmenti.

Un esempio pratico

Considero due angoli alfa e beta

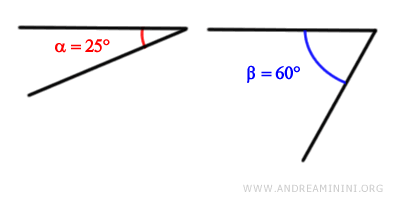
I due angoli sono di ampiezza non nulla.

$$ \alpha = 25° $$

$$ \beta = 60° $$

Inoltre, i due angoli sono non congruenti perché l'angolo beta è di ampiezza maggiore rispetto all'angolo alfa.

In questo caso esiste un multiplo dell'angolo minore (alfa) che supera l'angolo maggiore (beta).

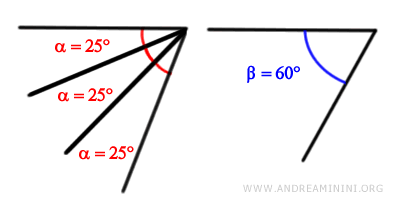
Si tratta del multiplo di 3 dell'angolo alfa

$$ 3 \cdot \alpha > \beta $$

$$ 3 \cdot 25° > 60° $$

$$ 75° > 60° $$

Pertanto, qualunque sia l'ampiezza di due angoli non congruenti, purché non nulli, è sempre possibile trovare un multiplo dell'angolo minore che supera l'ampiezza dell'angolo maggiore.

E così via.