Misura degli angoli in gradi, primi e secondi

La misura degli angoli in gradi (°), primi (′) e secondi (″) si ottiene seguendo questa suddivisione: $$ 1 \ \text{grado (°)} = 60 \ \text{primi (′)} $$ $$ 1 \ \text{primo (′)} = 60 \ \text{secondi (″)} $$

E' una rappresentazione alternativa del grado decimale.

Ad esempio, un angolo di 30° 15′ 20″ si legge:

• 30 gradi
• 15 primi
• 20 secondi

Questa rappresentazione è spesso utilizzata in navigazione e cartografia per misurare latitudine e longitudine, in astronomia per localizzare stelle e pianeti, in geometria e trigonometria per calcoli di angoli in triangoli.

Nota. Il grado decimale (es. 45,324°) è più pratico per i calcoli matematici, mentre i gradi, primi e secondi restano utili in ambiti tradizionali dove la precisione e la leggibilità sono fondamentali. Risale ai babilonesi che per primi utilizzarono il sistema sessagesimale, basato su 60, perché sessanta è un numero con molti divisori. E' stato poi utilizzato nella navigazione, nella lettura delle carte geografiche e in astronomia. In molti settori, oggi, i due sistemi convivono e si usano a seconda della necessità.

Conversione tra gradi decimali e gradi, primi, secondi

Talvolta, gli angoli sono espressi in forma decimale, per esempio 45.675°, e devo convertirli in gradi, primi e secondi o viceversa.

Da grado decimale a gradi, primi e secondi

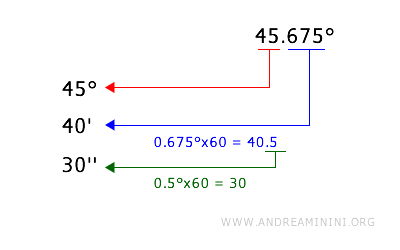
Per convertire un angolo in gradi decimali (es. 45.675°) in gradi, primi e secondi:

1. La parte intera è il numero di gradi (45°) e resta invariata.
2. Moltiplico la parte decimale per 60 per ottenere i primi: $$ 0.675 \times 60 = 40.5 $$ La parte intera del risultato è il numero di primi (40′).
3. Moltiplico la parte decimale rimanente per 60 per ottenere i secondi: $$ 0.5 \times 60 = 30 $$ La parte intera del risultato è il numero di secondi (30′).
4. L'ampiezza dell'angolo in gradi, minuti, secondi è 45° 40′ 30″.

Da gradi, primi e secondi a grado decimale

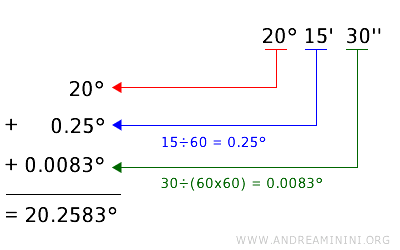
Per convertire un angolo da gradi, primi e secondi  (es. 20° 15′ 30″) in gradi decimali:

1. Lascio invariato il valore in gradi (20°)
2. Divido i primi per 60 e ottengo l'equivalente in gradi $$ 15′ = 15 \div 60 = 0.25° $$
3. Divido i secondi per 60 due volte di seguito, ossia li divido per 3600, per ottenere l'equivalente in gradi. $$ 30″ = 30 \div 3600 = 0.0083° $$
4. Sommo tutti i risultati in gradi $$ 20° + 0.25° + 0.0083° = 20.2583° $$
5. L'ampiezza dell'angolo in gradi decimali è 20.2583°

E così via.