Gli angoli supplementari
Gli angoli supplementari sono due angoli la cui somma è uguale a 180° (p radianti).
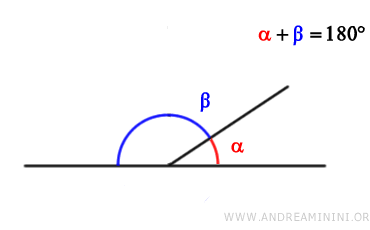
In altre parole, due angoli sono detti "supplementari" se la loro somma è uguale a un angolo piatto.
Questo vale indipendentemente dalla posizione o dall'orientamento degli angoli.
La definizione di angolo supplementare si applica solo a coppie di angoli. Pertanto, un singolo angolo non può definirsi supplementare. E' necessario avere due angoli.
Un esempio pratico
Considero due angoli
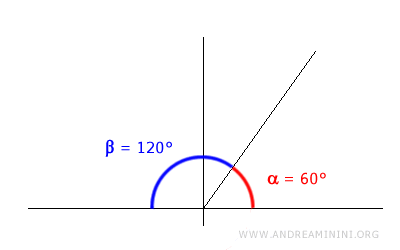
$$ \alpha = 60° $$
$$ \beta = 120° $$
Sono due angoli supplementari perché la somma delle loro ampiezze è uguale a 180°
$$ \alpha + \beta = 180° $$
Il risultato dell'addizione è un angolo piatto.
Osservazioni
Gli angoli supplementari hanno diverse proprietà interessanti:
- Ogni angolo è associato a un angolo supplementare
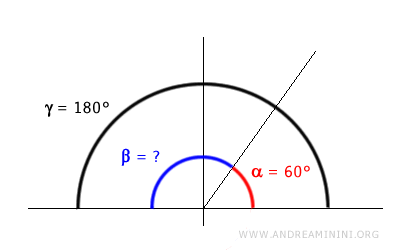
Dato un angolo, posso conoscere l'angolo supplementare sottraendo la sua ampiezza da 180 gradi. Ad esempio, se l'angolo alfa misura 120° gradi $$ \alpha = 120° $$ allora l'angolo supplementare beta è uguale a 60° $$ \beta = 180° - \alpha = 180° - 120° = 60° $$ Quindi, dato un angolo di ampiezza qualsiasi, si può sempre trovare l'altro angolo supplementare per differenza.
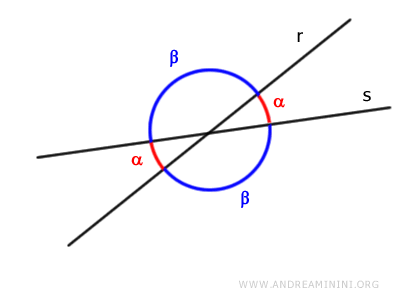
- Quando due rette si intersecano, gli angoli consecutivi presi a coppia sono angoli supplementari
Questa proprietà è spesso utilizzata nella risoluzione di problemi geometrici e nella dimostrazione di teoremi.
- Due angoli adiacenti sono sempre supplementari (e viceversa)
Due angoli sono detti "adiacenti" se sono consecutivi (ossia hanno un lato in comune) e i lati non comuni appartengono alla stessa retta. Quindi per ottenere l'angolo supplementare di un angolo dato, è sufficiente trovare il suo angolo adiacente.
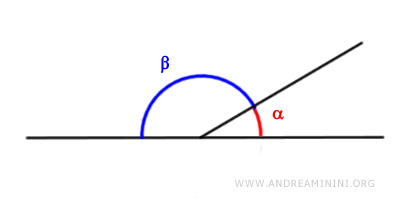
- Angoli supplementari a due angoli congruenti
Se due angoli $ \alpha $ e $ \alpha' $ sono supplementari rispettivamente a due angoli congruenti $ \beta \cong \beta' $ (o allo stesso angolo), allora sono congruenti $ \alpha \cong \alpha' $.
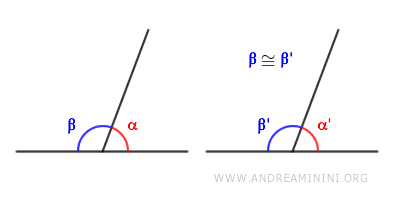
Dimostrazione. Siano \( \alpha \) e \( \alpha' \) due angoli tali che esistano due angoli \( \beta \) e \( \beta' \) rispettivamente supplementari ad essi, cioè: $$ \alpha + \beta = 180^\circ $$ $$ \alpha' + \beta' = 180^\circ $$ Per ipotesi gli angoli \( \beta \cong \beta' \) sono congruenti. Risolvo le due equazioni per ricavare $ \alpha $ e $ \beta $. $$ \alpha = 180^\circ - \beta $$ $$ \alpha' = 180^\circ - \beta' $$ Sapendo che \( \beta \cong \beta' \) sostituisco \( \beta \) con \( \beta' \) nella prima equazione. $$ \alpha = 180^\circ - \color{red}{ \beta' } $$$$ \alpha' = 180^\circ - \beta' $$ Poiché tutti gli angoli piatti (180°) sono congruenti tra loro e $ \beta \cong \beta' $ per ipotesi, deduco che \( \alpha \) è congruente a \( \alpha' \), ossia $ \alpha \cong \alpha' $ come volevo dimostrare.
E così via.
