Somma o sottrazione tra angoli congruenti
Se due angoli sono ottenuti come somma (o differenza) di coppie di angoli congruenti in modo corrispondente, allora anche gli angoli risultanti sono congruenti.
In altre parole se ho due coppie di angoli congruenti
$$ α ≅ β $$
$$ γ ≅ δ $$
Allora anche la somma degli angoli corrispondenti è la stessa.
$$ α + γ ≅ β + δ $$
Lo stesso vale per la differenza
$$ |α − γ| ≅ |β − δ| $$
La congruenza si conserva perché si tratta di operazioni su misure uguali:
Nota. Due angoli sono congruenti quando hanno la stessa ampiezza, ovvero quando coincidono perfettamente sovrapponendoli, indipendentemente dalla loro posizione nel piano.
Esempi pratici
Considero due coppie di angoli congruenti $ \alpha \cong \beta = 45° $ e $ \gamma \cong \delta = 30° $.
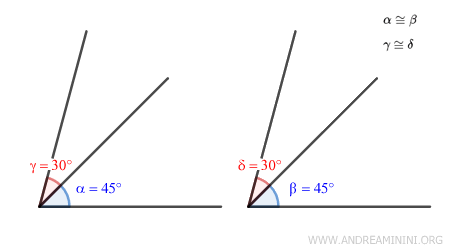
La somma degli angoli α + γ e = β + δ è la stessa ossia 75°
$$ α + γ = 45°+30° = 75° $$
$$ β + δ = 45°+30° =75° $$
Anche la sottrazione degli angoli α - γ e = β - δ è la stessa ossia 15°
$$ α - γ = 45° - 30° = 15° $$
$$ β - δ = 45° - 30° = 15° $$
Pertanto, la somma o la differenza ottenuta da coppie di angoli congruenti è ancora congruente.
Nota. Questa proprietà è molto utile in geometria, soprattutto quando si lavora con angoli ottenuti per costruzione o traslazione. Inoltre, mi permette di trattare le espressioni angolari in modo algebrico, senza preoccuparmi della loro posizione geometrica, ma solo della loro misura.
La dimostrazione
Considero due coppie di angoli congruenti
$$ \alpha \cong \beta $$
$$ \gamma \cong \delta $$
Scrivo la somma degli angoli non congruenti tra loro
$$ \alpha + \gamma $$
$$ \beta + \delta $$
Poiché $ \gamma \cong \delta $ per ipotesi iniziale, posso sostituirli tra loro nella somma $ \alpha + \gamma $.
$$ \alpha + \gamma = \alpha + \delta $$
Sapendo che anche $ \alpha \cong \beta $ per ipotesi iniziale, posso sostituirli tra loro in $ \alpha + \delta $
$$ \alpha + \gamma = \alpha + \delta = \beta + \delta $$
Ne consegue che le due somme hanno la stessa ampiezza
$$ \alpha + \gamma \cong \beta + \delta $$
Quindi, sono congruenti.
Nota. Lo stesso discorso può essere ripetuto nel caso della sottrazione. $$ \alpha - \gamma $$ $$ \beta - \delta $$ Sapendo che $ \gamma \cong \delta $ $$ \alpha - \gamma = \alpha - \delta $$ Sapendo che $ \alpha \cong \beta $ $$ \alpha - \gamma = \alpha - \delta = \beta - \delta $$ Pertanto, le due differenze hanno la stessa ampiezza. $$ \alpha - \gamma \cong \beta - \delta $$
Questo dimostra che la somma (o sottrazione) di angoli congruenti preserva la congruenza.
E così via.
