Angolo orientato
Cos'è un angolo orientato
Un angolo orientato è un angolo tra due lati associato a un senso di rotazione.
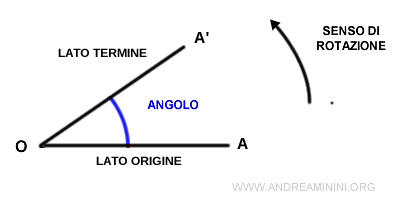
In un angolo orientato i lati sono considerati in un determinato ordine. Il lato iniziale è detto lato origine mentre il lato finale dopo la rotazione è detto lato termine.
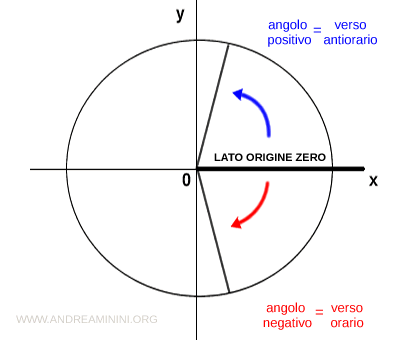
In generale, per convenzione l'angolo è positivo se la rotazione avviene in senso antiorario. Viceversa è negativo.
Come lato di origine zero si considera il semiasse positivo delle x del diagramma cartesiano.
Nota. Per indicare un angolo α minore di un angolo giro e tutti gli infiniti angoli orientati che ottengo dopo aver compiuto un angolo giro, uso la notazione in gradi $$ \alpha + k \cdot 360° \ \ \ con \ k \in Z $$ oppure in radianti $$ \alpha + k \cdot 2 \pi \ \ \ con \ k \in Z $$ Ad esempio, per indicare l'angolo α=800° utilizzo k=2 e scrivo $$ \alpha = 80° + 360 \cdot 2 $$
Un esempio pratico
Considero un angolo orientato come esempio.
$$ a \hat{O} b $$
Il lato iniziale è il lato "a" mentre quello finale è il lato "b". Il vertice è il punto O.
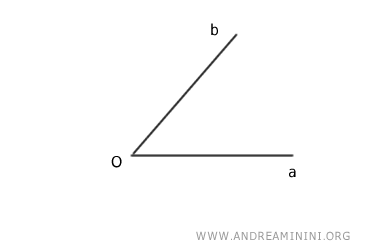
Qual è l'ampiezza di questo angolo orientato?
Essendo un angolo orientato, non posso affermare nulla perché non ho ancora indicato il verso dell'angolo.
Ci sono due possibilità alternative:
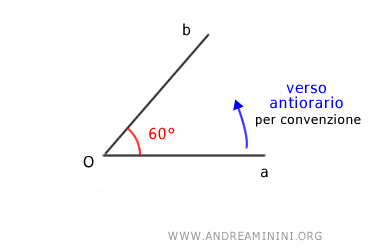
Se l'angolo è orientato in senso antiorario l'angolo ha un'ampiezza di 60°
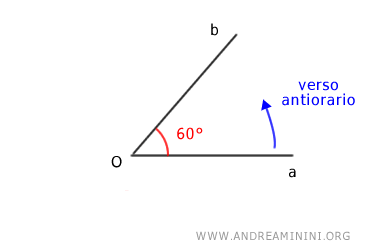
Viceversa, se l'angolo è orientato in senso orario l'angolo ha un ampiezza di 300°
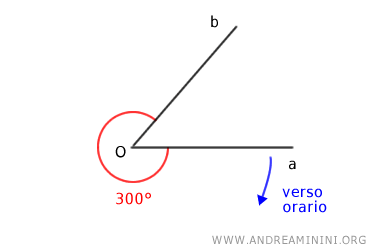
In entrambi i casi il lato "a" è il lato iniziale (o lato origine) dell'angolo orientato ma l'ampiezza è del tutto differente.
Quindi, l'ampiezza di un angolo orientato dipende esclusivamente dal verso che gli associo.
Nota. Per evitare questi problemi, quando in un angolo orientato non è indicato un verso, per misurare l'ampiezza si utilizza per convenzione il verso in senso antiorario. Pertanto, in questo esempio l'angolo orientato ha un'ampiezza di 60° per convenzione.
Gli angoli positivi e negativi
Il segno positivo o negativo di un angolo orientato dipende dal movmento del segmento OA e dal senso di rotazione adottato come sistema di riferimento
- Se adotto il verso di rotazione antiorario come riferimento, l'angolo orientato è positivo quando ruota in senso antiorario e negativo quando ruota in senso orario.
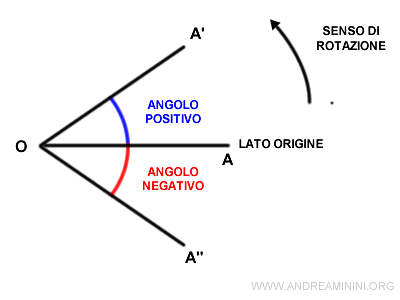
Nota. In questo caso la rotazione del segmento da OA a OA' è concorde con il senso di rotazione di riferimento. Quindi l'angolo è positivo. Viceversa, la rotazione del segmento da OA a OA" non è concorde e l'angolo è negativo.
- Se adotto il verso di rotazione orario come riferimento, l'angolo orientato è positivo quando ruota in senso orario e negativo quando ruota in senso antiorario.
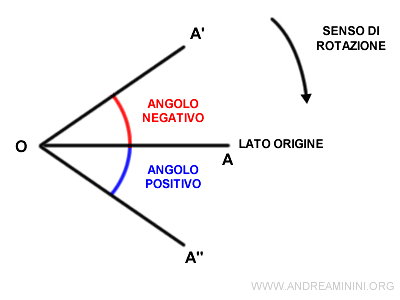
Nota. In questo caso la rotazione del segmento da OA a OA" è concorde con il senso di rotazione di riferimento. Quindi l'angolo è positivo. Viceversa, la rotazione del segmento da OA a OA' non è concorde e l'angolo è negativo.
Cosa accade se manca il senso di rotazione di riferimento?
Se non è specificato un verso di rotazione come sistema di riferimento, in fisica e matematica si adotta per convenzione il senso di rotazione antiorario con il lato di origine zero sul semiasse positivo delle ascisse (x).
Quindi, l'angolo orientato è positivo se il segmento ruota in senso antiorario. E viceversa.

A cosa servono gli angoli orientati?
In molti casi l'ampiezza di un angolo non mi fornisce tutte le informazioni di cui ho bisogno.
Ad esempio, devo girare il timone di 30°. Ma in quale direzione? Verso destra o verso sinistra?

Per saperlo devo prima fissare un verso di rotazione come sistema di riferimento.
Adotto il verso di rotazione antiorario.
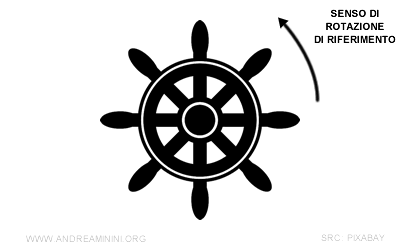
In questo modo posso capire il verso di rotazione.
Essendo 30° un numero positivo, vuol dire che la direzione è concorde al verso di rotazione.
Quindi, giro il timone in senso antiorario ossia verso sinistra.
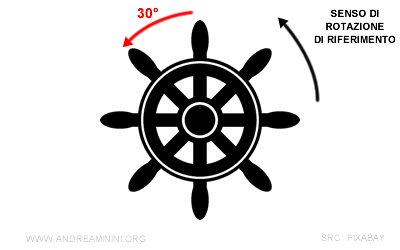
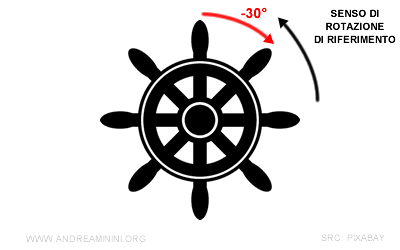
Se l'angolo orientato fosse stato pari a -30° avrei dovuto girare il timone verso destra, perché non concorde con il senso di rotazione di riferimento.
Le caratteristiche degli angoli orientati
Gli angoli orientati si distinguono per due caratteristiche
- Gli angoli orientati possono avere un'ampiezza anche negativa
Un angolo è negativo quando non è concorde con il senso di rotazione adottato come riferimento. Ad esempio un angolo di -20°.
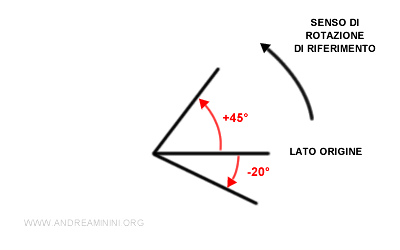
- Gli angoli orientati possono anche essere superiori all'angolo giro 360° (2π rad)
Ad esempio, un angolo orientato di 730° vuol dire che devo compiere due giri completi nel senso di rotazione adottato come riferimento e aggiungere altri 10° gradi.
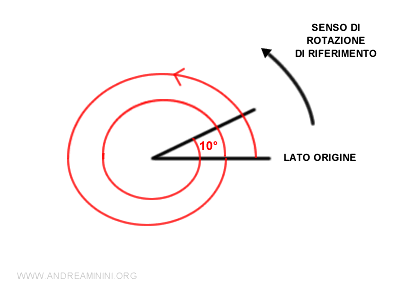
Dal punto di vista algebrico $$ 730° = 360° \cdot 2 + 10° $$ $$ 730° = 720° + 10° $$
La notazione sintetica degli angoli orientati
Un angolo orientato superiore a 360° può essere scritto in forma sintetica come somma di un angolo minore di 360° e un angolo giro moltiplicato per uno scalare k. $$ \alpha° + 360° \cdot k $$ Se l'angolo è in radianti si utilizza 2 pi greco.$$ \alpha + 2 \pi \cdot k $$ In entrambi i casi k è un numero intero.
Se k non è specificato, la notazione considera tutti gli angoli orientati che differiscono di un multiplo k dell'angolo giro.
Dove k è un numero intero positivo o negativo.
Esempio 1
L'angolo orientato di 730° può essere scritto in questo modo
$$ 730° = 360° \cdot 2 + 10° $$
Dove k=2
Esempio 2
Se non specifico lo scalare k
$$ \frac{ \pi }{ 2 } + k \cdot 2 \pi $$
la notazione indica tutti gli angoli di 90° (ossia π/2 ) multipli di un angolo giro (2π)
$$ \frac{ \pi }{ 2 } + k \cdot 2 \pi = \{ \frac{ \pi }{ 2 } \ , \ \frac{ \pi }{ 2 } \pm 2 \pi \ , \ \frac{ \pi }{ 2 } \pm 4 \pi \ , \ ... \} $$
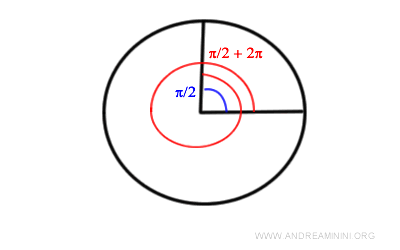
Ecco dal punto di vista grafico π/2 (blu) e π/2+2π (rosso).
Nel primo caso k = 0 mentre nel secondo k = 1.
E così via.
