Gli angoli supplementari, complementari ed esplementari
Due angoli sono detti complementari, supplementari o esplementari se la loro somma è congruente rispettivamente a un angolo retto, a un angolo piatto o a un angolo giro.
- Angoli complementari
Due angoli sono detti complementari se la somma delle loro misure è uguale a 90 gradi (π/2 in radianti).
In altre parole, se la somma di due angoli forma un angolo retto, allora sono angoli complementari.
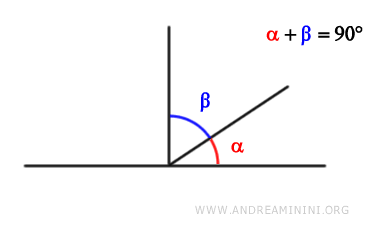
Ad esempio, se ho due angoli, uno di 30 gradi e l'altro di 60 gradi $$ \alpha=30° $$ $$ \beta=60° $$ questi sono angoli complementari perché la loro somma è 90 gradi $$ \alpha+\beta = 30° + 60° = 90° $$.
- Angoli supplementari
Due angoli sono detti supplementari se la somma delle loro misure è uguale a 180 gradi (π radianti).
In altre parole, se la somma di due angoli forma un angolo piatto, allora sono angoli supplementari.
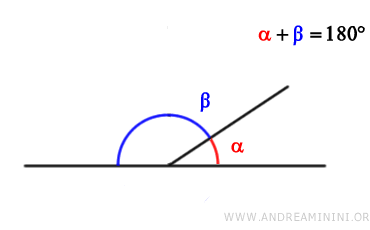
Ad esempio, se ho due angoli, uno di 120 gradi e l'altro di 60 gradi $$ \alpha=120° $$ $$ \beta=60° $$ questi sono angoli supplementari perché la loro somma è 180 gradi. $$ \alpha+\beta = 120° + 60° = 180° $$.
- Angoli esplementari
Due angoli sono detti esplementari se la somma delle loro ampiezze è uguale a 360° (2π in radianti).
In altre parole, se la somma di due angoli forma un angolo giro, ossia un cerchio completo, allora sono angoli esplementari.
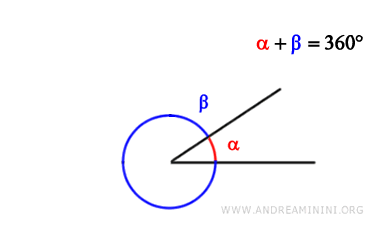
Ad esempio, se ho due angoli, uno di 270 gradi e l'altro di 90 gradi $$ \alpha=270° $$ $$ \beta=90° $$ questi sono angoli esplementari perché la loro somma è 360 gradi. $$ \alpha+\beta = 270° + 90° = 360° $$.
In sintesi, gli angoli complementari, supplementari ed esplementari sono classificati in base alla somma delle loro ampiezze. Gli angoli complementari sommano a 90°, gli angoli supplementari a 180°, e gli angoli esplementari a 360°.
Queste definizioni si applicano solo a coppie di angoli.
Pertanto, un singolo angolo non può essere definito come supplementare, complementare o esplementare senza riferimento a un altro angolo.
E così via.
