Gli angoli opposti al vertice
Due angoli sono detti angoli opposti al vertice se hanno in comune il vertice e i lati di ogni angolo sono il prolungamento dei lati dell'altro.
In altre parole, oltre ad avere il vertice in comune, i lati degli angoli appartengono alle stesse rette.
Un esempio pratico
Traccio due rette che si intersecano in un punto P.
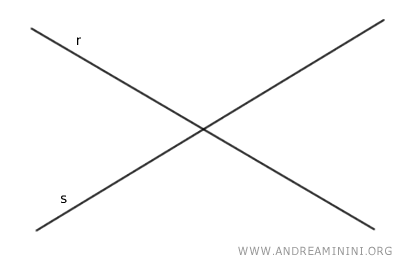
Le rette formano due angoli alfa e beta opposti al vertice P.
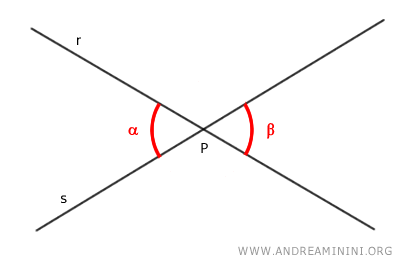
Osservazioni
Alcune osservazioni sugli angoli opposti al vertice.
- Gli angoli opposti al vertice sono congruenti.
Dimostrazione. Considero gli angoli alfa e beta opposti al vertice e un angolo gamma.
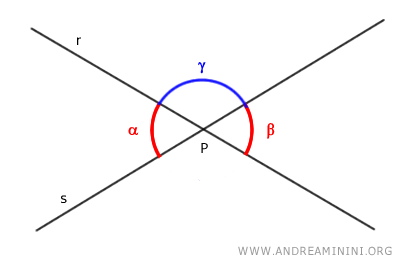
La somma dell'angolo alfa e gamma formano un angolo di 180° (angolo piatto). Quindi i due angoli alfa e gamma sono angoli adiacenti. $$ \alpha + \gamma = 180° $$ Allo stesso modo anche gli angoli beta e gamma sono angoli adiacenti perché sono consecutivi e la loro somma è pari a 180° $$ \beta + \gamma = 180° $$ Pertanto, ricavando gli angoli alfa e beta nelle due equazioni dimostro che i due angoli sono congruenti $$ \alpha = 180° - \gamma $$ $$ \beta = 180° - \gamma $$ - Angoli esterni
In un poligono due angoli esterni (βe e β'e) sullo stesso vertice (B) sono angoli opposti al vertice e sono fra loro congruenti βe≅β'e. Entrambi gli angoli sono supplementari con l'angolo interno (β) ovvero βe+β=180° e β'e+β=180°. Per questa ragione si parla genericamente di "angolo esterno" al vertice senza precisare a quale dei due ci si riferisce.
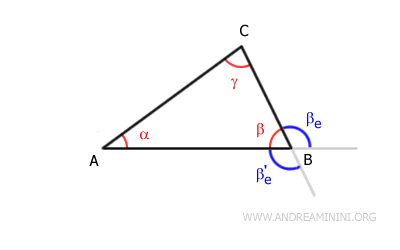
E così via.
