Gli angoli alterni

Date due rette "r" e "s" e una rette trasversale "t", due angoli sono detti angoli alterni se non hanno il vertice in comune e appartengono a semipiani opposti rispetto alla retta trasversale.

Gli angoli alterni possono essere

Angoli alterni interni
se si trovano tra le rette "r" e "s".
Angoli alterni esterni
se non si trovano tra le rette "r" e "s".

Un esempio pratico

Considero due rette "r" e "s".

Una retta "t" incide le due due rette "r" e "s" in due punti diversi.

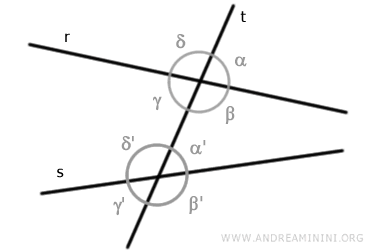
gli angoli alterni, coniugati e corrispondenti

Nei due punti di intersezione si formano due angoli giri.

Gli angoli (β,δ') di colore rosso sono angoli alterni interni, perché non hanno il vertice in comune e si trovano su semipiani opposti rispetto alla trasversale "t".

Inoltre, sono interni perché i due angoli si trovano tra le rette "r" e "s".

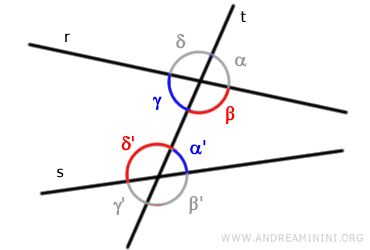
esempio di angoli alterni interni

Allo stesso modo, gli angoli (γ,α') di colore blu sono angoli alterni interni per le stesse ragioni.

Gli angoli (α,γ') di colore rosso sono angoli alterni esterni, perché non hanno il vertice in comune e si trovano su semipiani opposti rispetto alla trasversale "t".

Inoltre, sono esterni perché non si trovano tra le rette "r" e "s".

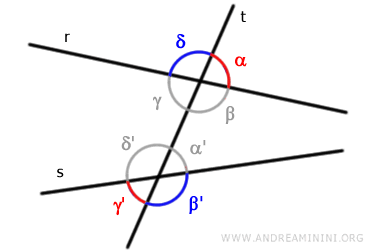
gli angoli alterni esterni

Per le stesse motivazioni, gli angoli (β',δ) di colore blu sono angoli alterni esterni.

E così via.