Lati concordi e discordi di un angolo

In due angoli con i lati paralleli, i lati sono detti

• lati concordi
  se si trovano nella stessa parte rispetto alla retta che congiunge i vertici dei due angoli
• lati discordi
  se si trovano in parti opposte rispetto alla retta che congiunge i vertici dei due angoli

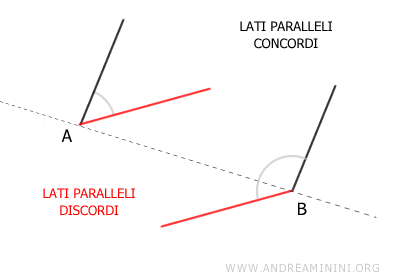
Se i lati paralleli di due angoli sono entrambi concordi o entrambi discordi, allora gli angoli sono congruenti. Se non lo sono, gli angoli sono supplementari, ovvero la loro somma è di 180°.

La spiegazione

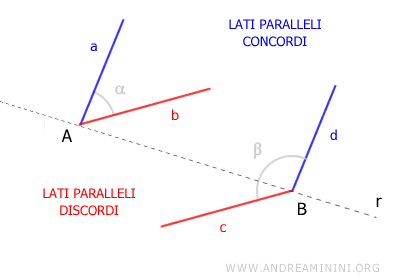
L'ipotesi di partenza è di avere due angoli con i lati paralleli tra loro.

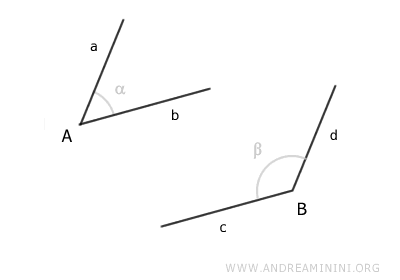
Traccio una retta r che passa per i vertici A e B dei due angoli.

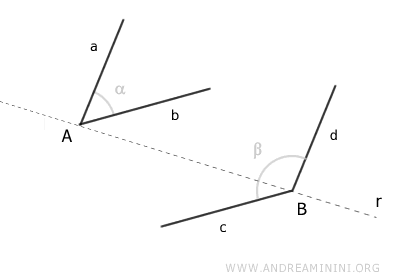
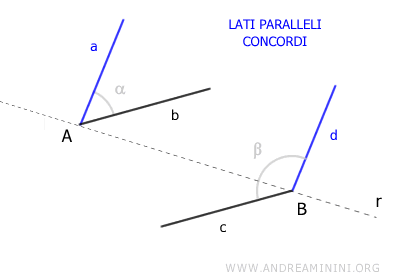
Se i lati paralleli di questi angoli sono entrambi alla stessa parte (sia a sinistra che a destra) di questa retta r, allora questi lati sono "concordi".

In questo caso i lati paralleli concordi sono i lati a e d

Se invece un lato è a sinistra e l'altro è a destra della retta r, allora questi lati paralleli sono lati "discordi".

In questo caso, sono lati paralleli discordi i lati b e c.

Osservazioni

Alcune osservazioni utili sui lati concordi e discordi di un angolo

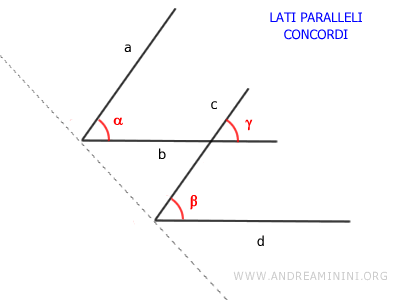
• Gli angoli con i lati paralleli sono congruenti se hanno tutti i lati paralleli concordi o discordi.

  Dimostrazione (lati concordi). Questi angoli hanno i lati paralleli a||c e b||d. Gli angoli β e γ sono angoli corrispondenti di due rette parallele b e d tagliate tagliate dalla retta c. Quindi, per il teorema delle rette parallele sono angoli congruenti β≅γ. Allo stesso modo anche gli angoli α e γ sono angoli corrispondenti delle rette parallele a e c tagliate dalla retta b. Quindi, sempre per il teorema delle rette parallele sono angoli congruenti α≅γ. Infine, per la proprietà transitiva se α≅γ e β≅γ allora anche gli angoli α e β sono angoli congruenti α≅β.
  
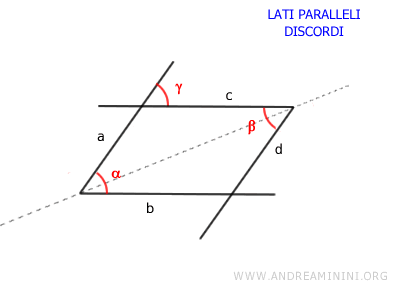
  Dimostrazione (lati discordi). Questi angoli hanno i lati paralleli a||d e b||c. Gli angoli β e γ sono angoli alterni interni di due rette parallele a e d tagliate tagliate dalla retta c. Pertanto, per il teorema delle rette parallele sono angoli congruenti β≅γ. Gli angoli α e γ, invece, sono angoli corrispondenti delle rette parallele c e b tagliate dalla retta a. Quindi, sempre per il teorema delle rette parallele sono angoli congruenti α≅γ. Infine, applico la proprietà transitiva: se α≅γ e β≅γ allora anche gli angoli α e β sono angoli congruenti α≅β.
  

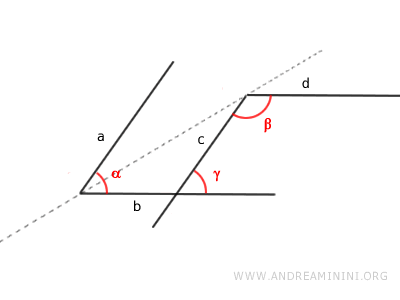
• Gli angoli con i lati paralleli sono supplementari se hanno due lati concordi e due lati discordi.
  

  Dimostrazione. Questi angoli hanno due lati paralleli discordi a||c e due lati paralleli concordi b||d. Gli angoli β e γ sono angoli coniugati di due rette parallele b e d tagliate tagliate dalla retta c. Quindi, per il teorema delle rette parallele sono angoli supplementari β+γ=180°. Gli angoli α e γ sono angoli corrispondenti delle rette parallele a e c tagliate dalla retta b. Quindi, per il teorema delle rette parallele sono angoli congruenti α≅γ. Infine, per la proprietà transitiva se α≅γ e β+γ=180° allora anche gli angoli α e β sono angoli supplementari α+β=180°.
  

E così via