L'assioma del trasporto degli angoli
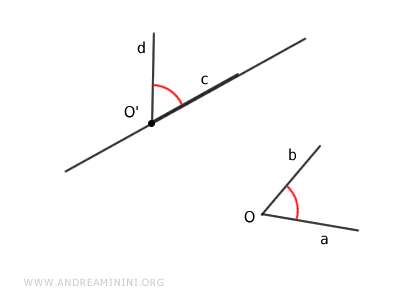
Data una semiretta di origine O' e un angolo aOb di origine O, fissato un verso di rotazione, esiste un unico angolo cO'd nel semipiano tale che i due angoli aOb e cO'c sono congruenti tra loro. $$ aOb \ \cong \ cO'd $$
L'assioma o postulato del trasporto degli angoli è un concetto molto importante della geometria euclidea perché stabilisce una proprietà fondamentale degli angoli.
In pratica, il postulato afferma che gli angoli possono essere trasportati, o copiati, da un punto a un altro mantenendo la loro ampiezza.
Ad esempio, se prendo un angolo e lo sposto con un movimento rigido (es. rotazione, traslazione, ecc.) senza modificarne l'ampiezza, il nuovo angolo ottenuto è congruente all'originale.
Nota. Questo postulato è una conseguenza del più ampio "Postulato delle trasformazioni rigide" o "Postulato di Euclide", che afferma che è possibile effettuare traslazioni, rotazioni e riflessioni nello spazio senza alterare le misure degli angoli.
E così via.
