Angoli corrispondenti

Gli angoli corrispondenti sono una coppia di angoli che non hanno il vertice in comune e si trovano nella stessa posizione relativa rispetto a due linee intersecate da una trasversale.

In altre parole, gli angoli corrispondenti sono angoli che si trovano nello stesso "posto".

In ogni coppia di angoli corrispondenti, un angolo è esterno mentre l'altro è interno.

Un esempio pratico

Ecco un esempio pratico.

Considero due rette “r” e “s” tagliate da una retta “t” in modo trasversale.

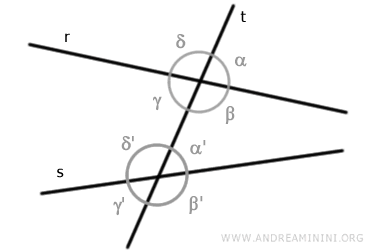
Le intersezioni tra la retta “t” e le altre due rette formano otto angoli: α, β, γ, δ, α', β', γ', δ'

Sono angoli corrispondenti le coppie di angoli che si trovano nella stessa posizione rispetto alla retta "t" e non hanno il vertice in comune

Ad esempio, gli angoli α e α' sono angoli corrispondenti.

L'angolo α si trova all'esterno delle rette mentre l'angolo α' all'interno.

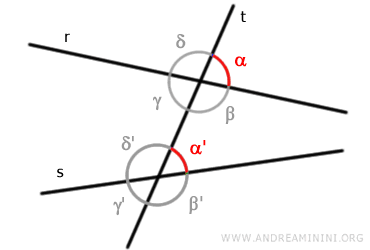
Anche gli angoli β e β' sono angoli corrispondenti.

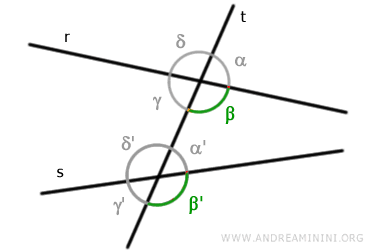
Allo stesso modo, gli angoli γ e γ' sono un'altra coppia di angoli corrispondenti.

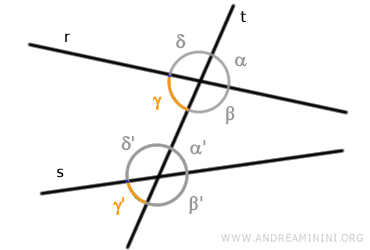
Infine, gli angoli δ e δ' sono l'ultima coppia di angoli corrispondenti.

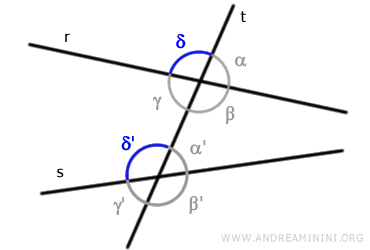
In tutti i casi, un angolo della coppia è interno alle rette "r" e "s" mentre l'altro angolo è esterno.

Il caso delle rette parallele

Quando le linee "r" e "s" sono parallele tra loro e sono intersecate da una trasversale "r", gli angoli corrispondenti sono anche congruenti ossia hanno la stessa misura.

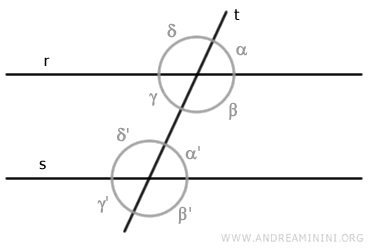
Ad esempio, in questo caso gli angoli α e α' non sono solo angoli corrispondenti ma anche congruenti, perché hanno la stessa ampiezza.

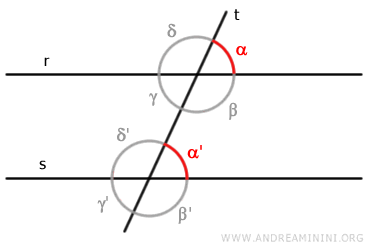
Quest'ultima è una delle proprietà fondamentali delle rette parallele nella geometria euclidea ed è spesso utilizzata nelle dimostrazioni geometriche e nei teoremi.