Intersezione di insiemi aperti nella topologia quoziente

Data l'intersezione finita di una collezione $ U_i $ di insiemi aperti nella topologia quoziente, la preimmagine dell'intersezione è uguale all'intersezione delle preimmagini degli insiemi degli insiemi che è un insieme aperto nella topologia di origine X. $$ p^{-1}( \bigcap U_i ) = \bigcap p^{-1}(U_i) $$ Pertanto, l'intersezione finita di insiemi aperti è un insieme aperto nella topologia quoziente.

Un esempio pratico

Considero il solito spazio quoziente $ A = \mathbb{R}/\mathbb{Z} $, che posso immaginare come un cerchio.

In questa topologia lo spazio di origine è l'insieme dei numeri reali $ \mathbb{R} $ e la mappa quoziente $ p: \mathbb{R} \to \mathbb{R}/\mathbb{Z} $ manda ogni numero reale al suo valore decimale.

Lo spazio della topologia quoziente è l'intervallo [0,1).

Ad esempio, l'immagine dei numeri 0.3, 1.3, 2.3 è sempre 0.3 sul cerchio.

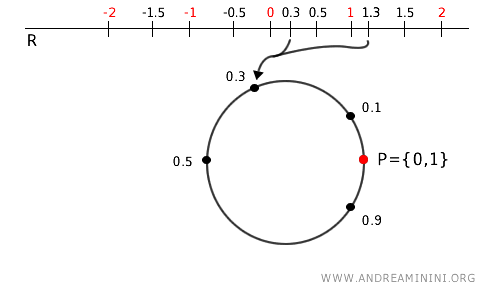
esempio

Prendo due insiemi aperti nel cerchio $ A $:

$$ U_1 = (0.1, 0.5) $$

$$ U_2 = (0.3, 0.7) $$

Questi intervalli sono aperti nella topologia quoziente $ \mathbb{R}/\mathbb{Z} $.

Ora faccio l'intersezione finita di questi due insiemi aperti:

$$ U_1 \cap U_2 = (0.3, 0.5) $$

L’intersezione è chiaramente aperta nel cerchio, perché è un intervallo aperto.

La preimmagine di questi insiemi sotto la mappa $ p $ in $ \mathbb{R} $ è un'unione infinita di intervalli aperti ripetuti lungo la retta reale.

La preimmagine di $ U_1 $ è:

$$ p^{-1}(U_1) = (0.1, 0.5) \cup (1.1, 1.5) \cup (2.1, 2.5) \cup \dots $$

La preimmagine di $ U_2 $ è:

$$ p^{-1}(U_2) = (0.3, 0.7) \cup (1.3, 1.7) \cup (2.3, 2.7) \cup \dots $$

A questo punto calcolo la preimmagine dell’intersezione.

La preimmagine di $ U_1 \cap U_2 $ in $ \mathbb{R} $ è l'intersezione delle preimmagini di $ U_1 $ e $ U_2 $:

$$ p^{-1}(U_1 \cap U_2) = (0.3, 0.5) \cup (1.3, 1.5) \cup (2.3, 2.5) \cup \dots $$

Questa è una unione di intervalli aperti nella topologia standard di $ \mathbb{R} $, quindi la preimmagine è aperta in $ \mathbb{R} $.

Dato che la preimmagine dell’intersezione è un insieme aperto in $ \mathbb{R} $, posso concludere che l’intersezione $ U_1 \cap U_2 $ è un insieme aperto nella topologia quoziente $ \mathbb{R}/\mathbb{Z} $.

Pertanto, l’intersezione finita di insiemi aperti nel cerchio è aperta, come previsto.

E così via.