Equazioni in seno e coseno di secondo grado
Un'equazione in seno e coseno di secondo grado si presenta in questa forma $$ a \sin^2 x + b \sin x \cos x + c \cos^2 x = d $$
Come risolvere le equazioni di secondo grado in seno e coseno
Un'equazione in secondo grado posso risolverla usando diverse tecniche a seconda se l'equazione è omogenea oppure no
Tecnica 1 (equazione omogena)
Se l'equazione goniometrica è omogenea (ossia il termine noto è nullo) e il coefficiente a è nullo, l'equazione si riduce a
$$ b \sin x \cos x + c \cos^2 x = 0$$
A questo punto mi basta mettere in evidenza il coseno
$$ \cos x (b \sin x + c \cos x) = 0 $$
Poi applico la legge di annullamento del prodotto e verifico in quali condizioni si annulla il primo fattore (cos x) e/o il secondo fattore (b sin x + c cos x).
Nota. La stessa tecnica la posso utilizzare nelle equazioni omogenee in cui il coefficiente c è nullo . $$ a \sin^2 x + b \sin x \cos x = 0 $$ In questo caso metto in evidenza la funzione seno $$ \sin x (a \sin x + b \cos x) = 0 $$ e, come nel caso precedente, cerco le soluzioni tramite la legge di annullamento del prodotto.
Tecnica 2 (equazione omogenea)
Per risolvere un'equazione omogenea di secondo grado in seno e coseno, divido l'equazione per la funzione coseno quadro (cos2 x)
$$ a \sin^2 x + b \sin x \cos x + c \cos^2 x = 0$$
$$ \frac{a \sin^2 x + b \sin x \cos x + c \cos^2 x}{\cos^2 x} = \frac{0}{\cos^2 x}$$
$$ \frac{a \sin^2 x}{\cos^2 x} + \frac{b \sin x \cos x}{\cos^2 x} + \frac{c \cos^2 x}{\cos^2 x} = 0 $$
$$ a \frac{\sin^2 x}{\cos^2 x} + b \frac{\sin x \cos x}{\cos x \cos x} + c = 0 $$
$$ a \frac{\sin^2 x}{\cos^2 x} + b \cdot \frac{\sin}{\cos x} \cdot \frac{\cos x}{\cos x} + c = 0 $$
$$ a \frac{\sin^2 x}{\cos^2 x} + b \cdot \frac{\sin}{\cos x} + c = 0 $$
Poi applico la seconda relazione fondamentale della trigonometria e sostituisco i rapporti sin/cos nella funzione tangente
$$ a \tan^2 x + b \cdot \tan x + c = 0 $$
Applico il metodo della sostituzione della variabile e sostituisco la funzione tangente con una variabile di comodo y = tan x
$$ a y^2 + b \cdot y + c = 0 $$
Poi risolvo l'equazione di 2° grado con la classica formula algebrica
$$ y = \frac{-b \pm \sqrt{b^2-4ac}}{2a} $$
Una volta trovate le soluzioni y1 e y2 dell'equazione, se esistono, trovo l'incognita x risolvendo le equazioni goniometriche elementari
$$ \tan x = y_1 $$
$$ \tan x = y_2 $$
In questo modo ho ricondotto l'equazione di secondo grado in seno e coseno in un'equazione goniometrica elementare.
Tecnica 3 (equazione non omogenea)
Se l'equazione di 2° non è omogenea, ossia il termine noto d≠0 è diverso da zero
$$ a \sin^2 x + b \sin x \cos x + c \cos^2 x = d $$
posso trasformarla in un'equazione di 2° omogenea equivalente moltiplicando il termine noto per 1
$$ a \sin^2 x + b \sin x \cos x + c \cos^2 x = d \cdot 1 $$
Secondo la prima relazione fondamentale della trigonometria sin2 x + cos2 x = 1
Quindi, nell'equazione posso sostituire 1 con sin2 x + cos2 x
$$ a \sin^2 x + b \sin x \cos x + c \cos^2 x = d \cdot (\sin^2 x + \cos^2 x) $$
$$ a \sin^2 x + b \sin x \cos x + c \cos^2 x - d \cdot (\sin^2 x + \cos^2 x) = 0 $$
In questo modo ho trasformato l'equazione di 2° grado in un'equazione omogenea equivalente che posso risolvere usando una delle precedenti tecniche (tecnica 1 o tecnica 2).
Un esempio pratico
Esempio 1
Devo risolvere l'equazione omogenea di secondo grado in seno e coseno
$$ \sin^2 x - \sqrt{3} \sin x \cos x = 0 $$
Essendo nullo il coefficiente del coseno quadro, questa equazione la risolvo con la legge di annullamento del prodotto.
Metto in evidenza la funzione trigonometrica seno.
$$ \sin x ( \sin x - \sqrt{3} \cos x ) = 0 $$
Poi verifico quando i due fattori sono nulli.
- L'equazione sin x = 0 è una equazione elementare del seno $$ \sin x = 0 $$ In questo caso la soluzione è molto semplice. L'equazione elementare sin x = 0 è nulla quando x = 0 + kπ. Quindi la prima soluzione dell'equazione di 2° grado è x = 0 + kπ
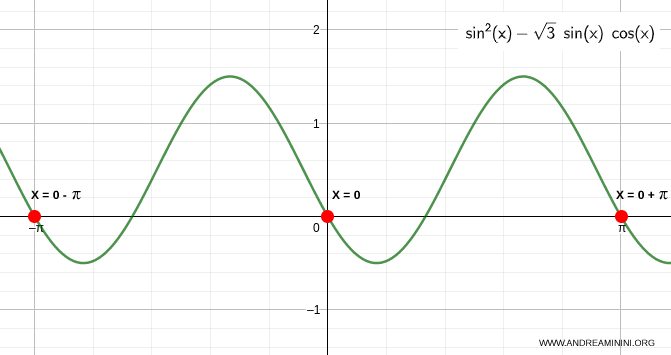
- L'equazione sin x - √3 cos x = 0 è un'equazione goniometrica di 1° grado. Quindi, la posso risolvere usando una delle tecniche di risoluzione delle equazioni goniometriche lineari. $$ \sin x - \sqrt{3} \cos x = 0 $$ Divido per il coseno $$ \frac{\sin x}{\cos x} - \sqrt{3} \frac{\cos x}{\cos x} = \frac{0}{\cos x} $$ $$ \tan x - \sqrt{3} = 0 $$ $$ \tan x = \sqrt{3} $$ L'equazione lineare diventa un'equazione elementare della tangente che è soddisfatta quando x =π/3 + kπ. Quindi la seconda soluzione dell'equazione di 2° è x = π/3 + kπ
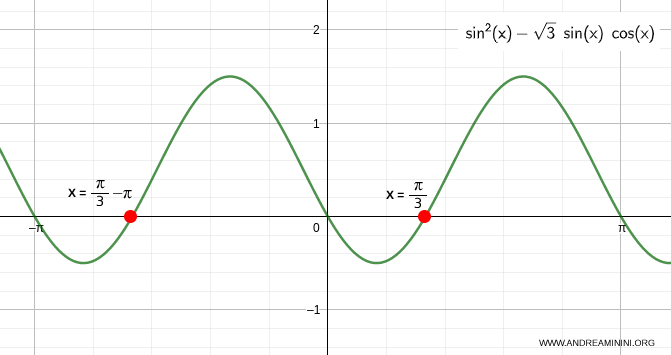
Pertanto, le soluzioni dell'equazione di 2° in seno e coseno sono
$$ x = 0 + k \pi \ \ ∨ \ \ \frac{\pi}{3} + k \pi$$
Esempio 2
Devo risolvere l'equazione di 2° grado in seno e coseno
$$ \sin^2 x + 2 \sin x \cos x - \cos^2 x = 0 $$
Si tratta di un'equazione omogenea.
I coefficienti sono non nulli, quindi la risolvo usando il metodo della sostituzione della variabile (tecnica 2).
Divido l'equazione per cos2 x
$$ \frac{ \sin^2 x + 2 \sin x \cos x - \cos^2 x }{\cos^2 x} = \frac{0}{\cos^2 x} $$
$$ \frac{ \sin^2 x}{\cos^2 x} + 2 \frac{ \sin x \cos x }{\cos^2 x} - \frac{\cos^2 x }{\cos^2 x} = 0 $$
$$ \frac{ \sin^2 x}{\cos^2 x} + 2 \frac{ \sin x \cos x }{\cos x \cos x} - 1 = 0 $$
$$ \frac{ \sin^2 x}{\cos^2 x} + 2 \frac{ \sin x }{ \cos x} - 1 = 0 $$
Per la seconda relazione fondamentale della trigonometria il rapporto sin x / cos x = tan x è la funzione tangente
$$ \tan^2 x + 2 \tan x - 1 = 0 $$
Così facendo ho ottenuto un'equazione equivalente di 2° grado con una sola funzione trigonometrica.
Sostituisco la funzione tangente con una variabile di comodo y=tan x
$$ y^2 + 2 y - 1 = 0 $$
Poi risolvo l'equazione di 2° grado nella variabile y
$$ y = \frac{-b \pm \sqrt{b^2-4ac}}{2a} $$
$$ y = \frac{-2 \pm \sqrt{2^2-4(1)(-1)}}{2(1)} $$
$$ y = \frac{-2 \pm \sqrt{4+4}}{2} $$
$$ y = \frac{-2 \pm \sqrt{8}}{2} $$
Semplifico dividendo tutto per 2
$$ y = \frac{- \frac{2}{2} \pm \frac{ \sqrt{8} }{2} }{ \frac{2}{2}} $$
$$ y = \frac{- \frac{2}{2} \pm \frac{ \sqrt{8} }{2} }{ \frac{2}{2}} $$
$$ y = \frac{- 1 \pm \sqrt{ \frac{8}{4} } }{ 1 } $$
$$ y = - 1 \pm \sqrt{2} $$
Quindi le soluzioni sono
$$ y = \begin{cases} -1 + \sqrt{2} \\ \\ -1 - \sqrt{2} \end{cases} $$
Sapendo che y=tan x allora
$$ \tan x = \begin{cases} -1 + \sqrt{2} \\ \\ -1 - \sqrt{2} \end{cases} $$
Ho così ridotto l'equazione di 2° grado a una equazione goniometrica elementare della tangente
A questo punto per trovare l'incognita x calcolo l'arcotangente delle soluzioni
$$ \arctan{ \tan x } = \begin{cases} \arctan{ -1 + \sqrt{2} } \\ \\ \arctan{ -1 - \sqrt{2} } \end{cases} $$
$$ x = \begin{cases} \arctan{ -1 + \sqrt{2} } \\ \\ \arctan{ -1 - \sqrt{2} } \end{cases} $$
Le soluzioni delle equazioni elementari sono x=π/8+kπ/2 e x=-π/8+kπ/2
$$ x = \begin{cases} \frac{\pi}{8} \\ \\ - \frac{\pi}{8} \end{cases} $$
Essendo k un numero intero qualsiasi posso unificare le due soluzioni in una sola soluzione x=π/8+kπ/2 dove k è un intero positivo, nullo o negativo.
Quiindi la soluzione dell'equazione di 2° grado è
$$ x = \frac{\pi}{8} + k \frac{\pi}{2} $$
Dal punto di vista grafico
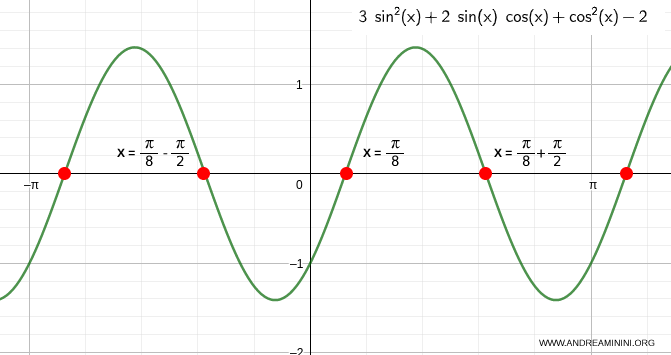
Esempio 3
Devo risolvere l'equazione di 2° grado in seno e coseno
$$ 3 \sin^2 x + 2 \sin x \cos x + \cos^2 = 2 $$
Si tratta di un'equazione non omogenea.
Quindi, devo prima trasformarla in un'equazione omogenea tramite la tecnica 3.
$$ 3 \sin^2 x + 2 \sin x \cos x + \cos^2 = 2 $$
La riscrivo in una forma equivalente
$$ 3 \sin^2 x + 2 \sin x \cos x + \cos^2 = 2 \cdot 1 $$
Secondo la prima relazione fondamentale della trigonometria sin2 x + cos2 x = 1
Pertanto, posso sostituire 1 con sin2 x + cos2 x
$$ 3 \sin^2 x + 2 \sin x \cos x + \cos^2 = 2 \cdot ( \sin^2 x + \cos^2 x) $$
$$ 3 \sin^2 x + 2 \sin x \cos x + \cos^2 - 2 \cdot ( \sin^2 x + \cos^2 x) = 0 $$
$$ 3 \sin^2 x + 2 \sin x \cos x + \cos^2 - 2 \sin^2 x - 2 \cos^2 x = 0 $$
$$ \sin^2 x + 2 \sin x \cos x - \cos^2 x = 0 $$
In questo modo ottengo un'equazione omogenea di 2° grado equivalente alla precedente.
Posso così risolverla con una tecnica di risoluzione delle equazioni omogenee.
Nota. La continuazione di questo esercizio è uguale all'esercizio 2. Pertanto, evito di riscriverlo.
E così via.
