Equazione goniometrica tan x = c
L'equazione goniometrica $$ \tan x=c $$ è un'equazione goniometrica elementare in cui l'incognita x è l'argomento della funzione tangente mentre c è un numero reale qualsiasi.
L'equazione tan x = c è sempre determinata e ammette infinite soluzioni del tipo α+kπ
$$ x = \alpha + k \pi $$
Nota. L'equazione tan x = c è determinata per qualsiasi valore c perché il codominio della funzione tangente ( -∞ , +∞ ) coincide con l'insieme dei numeri reali.
Per risolvere l'equazione trovo l'angolo α tramite la funzione inversa della tangente ossia l'arcotangente.
$$ \arctan c = \alpha $$
L'arcotangente calcola l'angolo α che determina il valore tan α = c.
Un esempio pratico
Devo verificare se questa equazione goniometrica ammette soluzioni
$$ \tan x = 1 $$
L'equazione è sempre determinata per qualsiasi numero reale e ha le seguenti soluzioni
$$ x = \alpha + k \pi $$
Per trovare l'angolo α calcolo l'arcotangente di 1 che è pari a π/4 (ossia 45°)
$$ \arctan 1 = \frac{\pi}{4} $$
Sostituisco l'angolo α=π/4 nella formula delle soluzioni dell'equazione goniometrica
$$ x = \alpha + k \pi $$
$$ x = \frac{\pi}{4} + k \pi $$
Dal punto di vista grafico la soluzione è la seguente
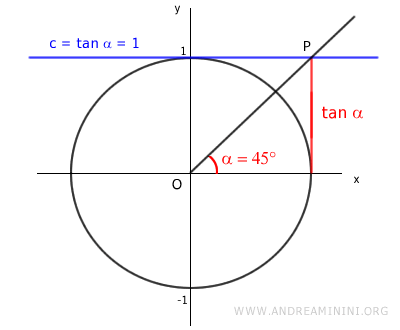
Per l'angolo π/4 rad (45°) l'equazione tan x = 1 è soddisfatta.
Essendo la tangente una funzione periodica considero anche i multipli interi k dell'angolo piatto π tra le soluzioni possibili.
$$ x = \frac{\pi}{4} + k \pi $$
Ad esempio, l'equazione goniometrica tan x = 1 è soddisfatta anche per π/4+π rad (ossia 45°+180°).
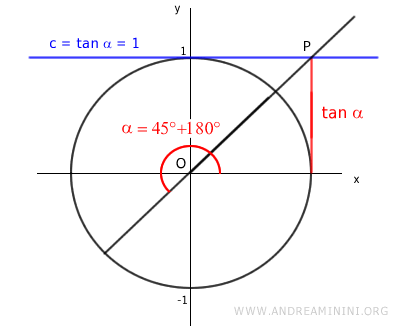
E così per qualsiasi altro multiplo intero kπ. Dove k è un numero intero qualsiasi positivo o negativo.
Pertanto, l'equazione goniometrica tan x = 1 ha infinite soluzioni del tipo π/4+kπ
La dimostrazione
Disegno la circonferenza goniometrica sul piano cartesiano.
La circonferenza goniometrica è una circonferenza con raggio pari a 1.
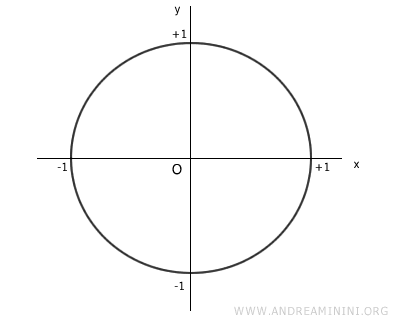
Il valore della funzione tangente si misura sull'asse verticale delle ordinate ed è compreso tra -∞ e +∞ (codominio della tangente).
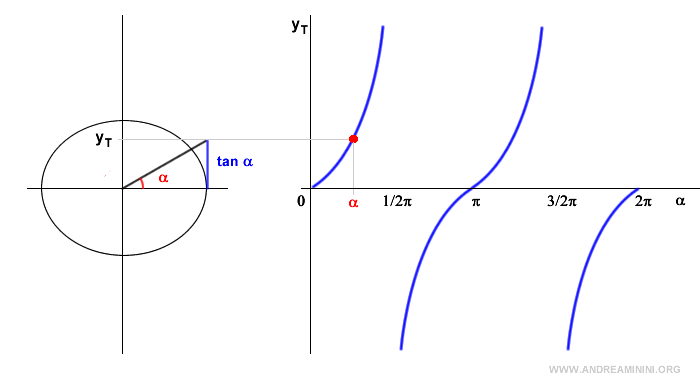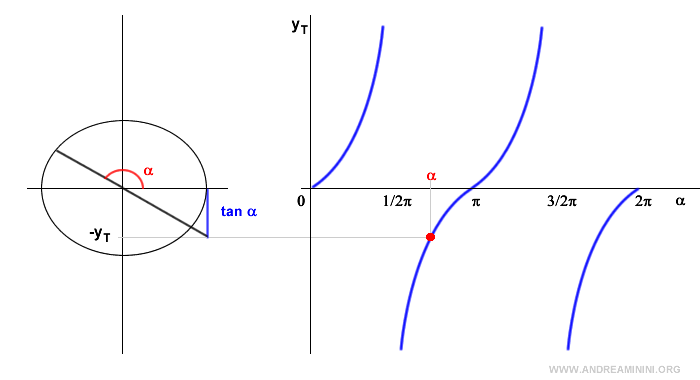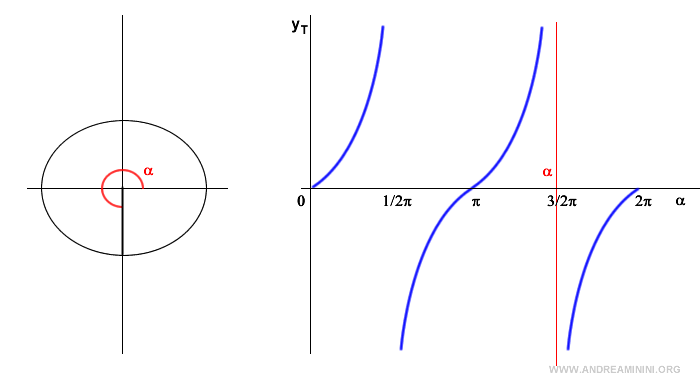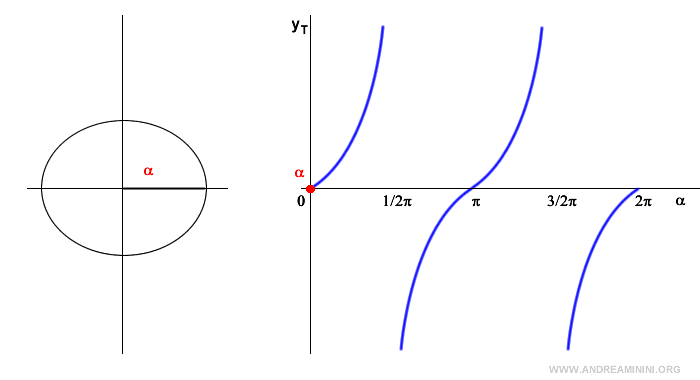
Considero un valore reale c qualsiasi e studio se l'equazione goniometrica ha soluzioni.
Qualunque sia il valore c scelto, positivo o negativo, la retta y=c è una retta parallela all'asse delle ascisse che interseca tangente in un punto P.
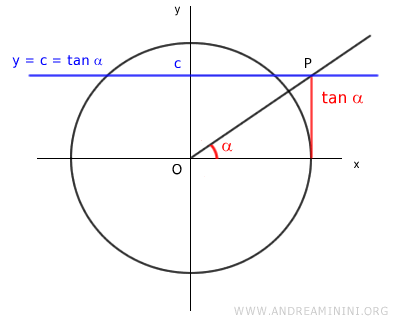
La tangente è definita anche per valori superiori al raggio della circonferenza goniometrica.
Quindi può assumere valori superiori a 1 e inferiori a -1.
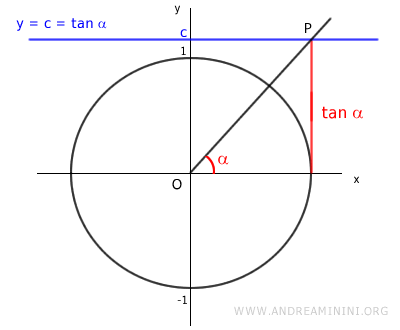
L'equazione goniometrica tan x = c è definita anche per qualsiasi valore negativo di c.
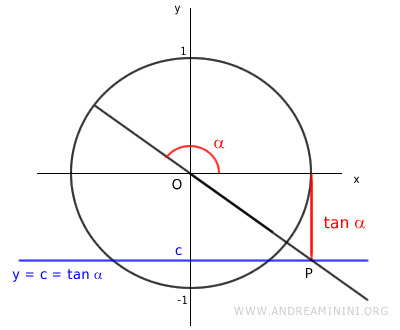
Pertanto, non esiste un valore c in cui l'equazione goniometrica tan x = c non è determinata.
Per qualsiasi valore c esiste un angolo α in grado di soddisfare l'equazione goniometrica tan x = c
$$ \tan \alpha = c $$
Tuttavia, questa non è l'unica soluzione possibile.
La tangente è una funzione periodica con periodo π che ripete gli stessi valori.
Quindi devo considerare nell'insieme delle soluzioni anche la somma dell'angolo α con i multipli interi k di π
$$ x = \alpha + k \cdot \pi $$
Come si trova l'angolo?
Per trovare l'angolo α applico la funzione arcotangente a entrambi i membri dell'equazione goniometrica tan x = c
$$ \arctan( \tan x ) = \arctan c $$
L'arcotangente è la funzione inversa della tangente.
Quindi, arctan(tan x) = x
$$ x = \arctan c $$
In questo modo trovo l'angolo x che determina il valore c = tan x della tangente.
E così via.
