Equazione goniometrica sin x = c
L'equazione goniometrica $$ \sin x=c $$ è un'equazione goniometrica elementare in cui l'incognita x è l'argomento della funzione seno mentre c è un numero reale qualsiasi.
Questa equazione è determinata solo se il termine noto c è compreso nell'intervallo reale c ∈ [-1,1]
$$ -1 \le c \le 1 $$
Al di fuori dell'intervallo chiuso [-1,1] l'equazione è impossibile da risolvere perché non coincide con il codominio della funzione seno.
Nota. In trigonometria la funzione seno assume valori compresi tra -1 e 1.
Se l’equazione è determinata ammette infinite soluzioni α+2πk oppure π-α+2πk.
$$ x = \alpha + 2\pi k \vee (\pi - \alpha) + 2\pi k $$
Per risolvere l'equazione trovo l'angolo α tramite la funzione inversa del seno ossia l'arcoseno.
$$ \arcsin c = \alpha $$
L'arcoseno calcola l'angolo α che determina il valore sin α = c.
Un esempio pratico
Devo verificare se questa equazione goniometrica ammette soluzioni
$$ \sin x = \frac{1}{2} $$
L'equazione è determinata perché il termine noto appartiene al codominio del seno.
$$ -1 \le \frac{1}{2} \le 1 $$
Quindi, l'equazione ha le seguenti soluzioni
$$ x = \alpha + 2\pi k \vee (\pi - \alpha) + 2\pi k $$
Per trovare l'angolo α calcolo l'arcoseno di 1/2 che è pari a π/6 (ossia 30°)
$$ \arcsin \frac{1}{2} = \frac{\pi}{6} $$
Sostituisco l'angolo α=π/6 nella formula delle soluzioni dell'equazione goniometrica
$$ x = \alpha + 2\pi k \vee (\pi - \alpha) + 2\pi k $$
$$ x = \frac{\pi}{6} + 2\pi k \vee (\pi - \frac{\pi}{6}) + 2\pi k $$
Dal punto di vista grafico le soluzioni sono le seguenti
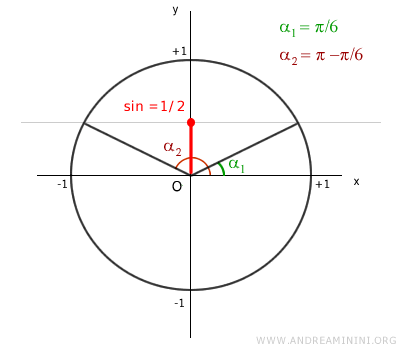
Sia per un angolo π/6 che per un angolo π-π/6 l'equazione sin x = 1/2 è soddisfatta.
Essendo il seno una funzione periodica devo considerare anche i multipli interi k di un angolo giro 2πk tra le soluzioni possibili.
$$ x = \frac{\pi}{6} + 2\pi k \vee (\pi - \frac{\pi}{6}) + 2\pi k $$
Pertanto, l'equazione goniometrica sin x = 1/2 ha infinite soluzioni del tipo π/6+2πk e π-π/6+2πk
La dimostrazione
Disegno la circonferenza goniometrica sul piano cartesiano.
La circonferenza goniometrica è una circonferenza con raggio pari a 1.
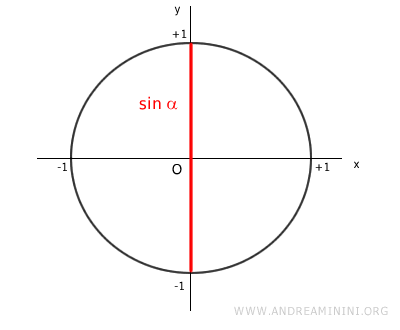
Il valore della funzione seno si misura sull'asse verticale delle ordinate ed è compreso tra -1 e +1 (codominio del seno).
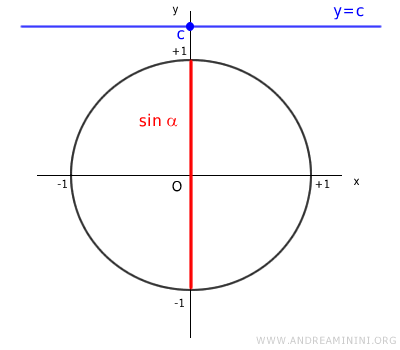
Prendo un valore reale c qualsiasi e studio se l'equazione goniometrica ha soluzioni.
Se il valore c è maggiore di 1, la retta y=c è una retta parallela all'asse delle ascisse che non interseca la circonferenza goniometrica.
Pertanto, nessun angolo x del seno può generare un valore c maggiore di uno.
Allo stesso modo, se il valore c è minore di -1, nessun angolo x del seno può generare il valore c.
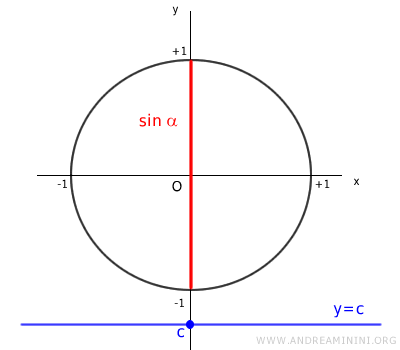
Pertanto, l'equazione sin x=c è determinata solo se il valore c è compreso nell'intervallo [-1,1]
$$ -1 \le c \le 1 $$
A questo punto considero un valore c nell'intervallo [-1,1].
L'equazione y=c è una retta parallela all'asse orizzontale che interseca la circonferenza goniometrica in due punti P1 e P2.
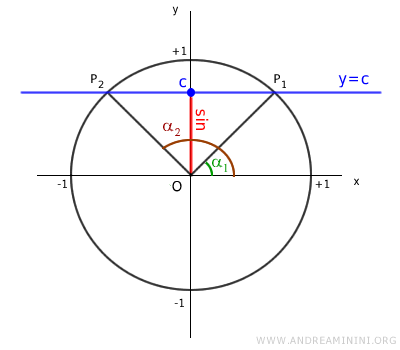
I punti P1 e P2 sono i lati terminali del raggio dell'angolo α1 e dell'angolo α2.
Pertanto, in corrispondenza del valore c esistono due angoli α1 e α2 in grado di soddisfare l'equazione goniometrica sin x = c
$$ \sin \alpha_1 = \sin \alpha_2 = c $$
Entrambe le soluzioni α1 e α2 soddisfano l'equazione, quindi posso scrivere
$$ x = \alpha_1 \vee \alpha_2 $$
Tuttavia, queste non sono le uniche soluzioni possibili.
Il seno è una funzione periodica che ripete gli stessi valori ogni k periodo 2π.
Quindi devo considerare nell'insieme delle soluzioni anche la somma di α1 e α2 con i multipli interi di 2πk
$$ x = \alpha_1 + 2\pi k \vee \alpha_2 + 2\pi k $$
Gli angoli α1 e α2 sono angoli associati del seno perché generano lo stesso risultato sin(α1)=sin(α2).
Quindi, posso riscrivere l'angolo α2=π-α1 in funzione di α1.
$$ x = \alpha_1 + 2\pi k \vee (\pi - \alpha1) + 2\pi k $$
Essendoci un solo angolo α1, semplifico ulteriormente l'equazione scrivendo α=α1
$$ x = \alpha + 2\pi k \vee (\pi - \alpha) + 2\pi k $$
Pertanto, se il valore c è compreso nell'intervallo [-1,1] l'equazione sin x = c è determinata e ammette infinite soluzioni x = α+2πk oppure π-α+2πk.
$$ \sin x = c $$
Nota. Nel caso particolare in cui c=1 o c=-1 la retta y=c interseca la circonferenza goniometrica in un solo punto anziché due. L'insieme delle soluzioni include anche questi casi particolari in cui $$ \alpha = \pi - \alpha $$
Per trovare l'angolo α applico la funzione arcoseno a entrambi i membri dell'equazione
$$ \arcsin( \sin x ) = \arcsin c $$
L'arcoseno è la funzione inversa del seno.
Quindi, arcsin(sin x) = x
$$ x = \arcsin c $$
In questo modo trovo la soluzione x dell'equazione goniometrica sin x = c.
E così via.
