Equazione goniometrica lineare in seno e coseno
Un'equazione goniometrica è detta equazione lineare in seno e coseno quando si può scrivere nella forma $$ a \sin x + b \cos x +c = 0 $$ Dove a,b,c sono coefficienti reali con a≠0 e b≠0.
Come risolvere le equazioni lineari
Queste equazioni posso risolverle facilmente riconducendo l'equazione a una forma elementare tramite il metodo algebrico.
- Se il termine noto è nullo (c=0) basta dividere l'equazione per il coseno. In questo modo l'equazione si trasforma in un'equazione goniometrica elementare nella tangente. $$ a \sin x + b \cos x = 0 $$ $$ a \frac{\sin x}{\cos x} + b \frac{\cos x}{\cos x} = \frac{0}{\cos x} $$ $$ a \tan x + b = 0 $$ $$ \tan x = - \frac{b}{a} $$
- Se il termine noto non è nullo (c≠0) uso le formule parametriche. $$ a \sin x + b \cos x + c = 0 $$ $$ a \frac{2t}{1+t^2} + \frac{1-t^2}{1+t^2} -1 = 0 $$ Dove la variabile t è $$ t = \tan \frac{x}{2} $$ La tangente non è definita per π radianti (180°). Pertanto, l'equazione non deve avere soluzioni in $$ x \ne \pi +2k \pi $$
Nota. In alternativa, posso sostituire il seno in coseno tramite il principio fondamentale della trigonometria. $$ \sin^2 x + \cos^2 x = 1 $$ ossia $$ \sin x = \pm \sqrt{1-\cos^2 x} $$ $$ \cos x = \pm \sqrt{1-\sin^2 x} $$
Un esempio pratico
Devo risolvere l'equazione goniometrica
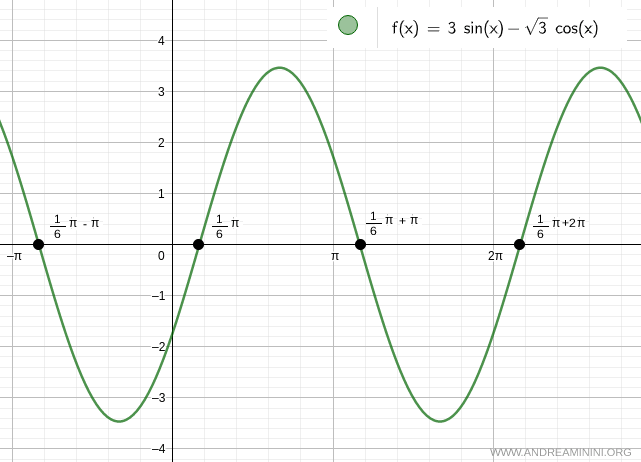
$$ 3 \sin x - \sqrt{3} \cos x = 0 $$
E' un'equazione lineare in seno e coseno con termine noto nullo (c=0).
Divido per cos x per trasformare l'equazione goniometrica in una equazione in forma elementare nella tangente
$$ 3 \frac{ \sin x }{ \cos x} - \sqrt{3} \frac{ \cos x }{ \cos x} = \frac{ 0 }{ \cos x} $$
$$ 3 \tan x - \sqrt{3} = 0 $$
Metto in evidenza la tangente
$$ \tan x = \frac{\sqrt{3}}{3} $$
Infine calcolo il valore dell'incognita x applicando l'arcotangente a entrambi i membri dell'equazione
$$ \arctan( \tan x ) = \arctan( \frac{\sqrt{3}}{3} ) $$
$$ x = \arctan( \frac{\sqrt{3}}{3} ) $$
L'arcotangente di rad(3)/3 è π/6
$$ x = \frac{\pi}{6} $$
Poiché la tangente è una funzione periodica con periodo π, ossia 180°, esistono infinite soluzioni ogni k angolo piatto (π).
$$ x = \frac{\pi}{6} + k \pi $$
Dove k è un numero intero qualsiasi.
Esempio 2
Devo risolvere l'equazione goniometrica
$$ 2 \sin x - 3 \cos x -1 = $$
E' un'equazione lineare in seno e coseno.
Verifico se x=π/2 è una soluzione dell'equazione
$$ 2 \sin (\frac{\pi}{2}) - 3 \cos (\frac{\pi}{2}) -1 = 0 $$
$$ 2 \cdot 1 - 3 \cdot 0 - 1 = 0 $$
$$ 2 - 1 = 0 $$
$$ 1 = 0 $$
Pi greco mezzi non è una soluzione dell'equazione, quindi posso procedere.
Sostituisco il seno e il coseno con le rispettive formule parametriche, dove t=tan(x/2)
$$ a \frac{2t}{1+t^2} + b \frac{1-t^2}{1+t^2} +c = 0 $$
Dove a = 2, b=-3, c=-1
$$ 2 \frac{2t}{1+t^2} -3 \frac{1-t^2}{1+t^2} -1 = 0 $$
Semplifico l'equazione
$$ \frac{4t-3+3t^2-(1+t^2)}{1+t^2} = 0 $$
$$ \frac{4t-3+3t^2-1-t^2}{1+t^2} = 0 $$
$$ \frac{2t^2+4t-4}{1+t^2} = 0 $$
Moltiplico entrambi i membri dell'equazione per (1+t2)
$$ (1+t^2) \cdot \frac{2t^2+4t-4}{1+t^2} = 0 \cdot (1+t^2) $$
$$ 2t^2+4t-4 = 0 $$
Divido entrambi i membri dell'equazione per 2
$$ \frac{2t^2+4t-4}{2} = \frac{0}{2} $$
$$ t^2+2t-2 = 0 $$
Infine risolvo l'equazione di 2° grado
$$ t = \frac{-b \pm \sqrt{b^2-4ac}}{2a} $$
$$ t = \frac{-2 \pm \sqrt{2^2-4(1)(-2)}}{2(1)} $$
$$ t = \frac{-2 \pm \sqrt{4+8}}{2} $$
$$ t = \frac{-2 \pm \sqrt{12}}{2} = \begin{cases} t_1 = \frac{-2 + \sqrt{12}}{2} \\ \\ t_2 = \frac{-2 - \sqrt{12}}{2} \end{cases} $$
Sapendo che t=tan x/2 la prima soluzione è un'equazione goniometrica elementare del tipo tan α = c
$$ \tan \frac{x}{2} = \frac{-2 + \sqrt{12}}{2} $$
Calcolo l'arcotangente a entrambi i membri
$$ \arctan ( \tan \frac{x}{2} ) = \arctan ( \frac{-2 + \sqrt{12}}{2} ) $$
$$ \frac{x}{2} = \arctan ( \frac{-2 + \sqrt{12}}{2} ) $$
A cui aggiungo kπ per includere anche le altre soluzioni con k intero
$$ \frac{x}{2} = \arctan ( \frac{-2 + \sqrt{12}}{2} ) + k \pi $$
L'arcotangente nel membro di destra è 0,63 radianti (36,21°)
$$ \frac{x}{2} = 0,63 \ rad + k \pi $$
$$ x = 1,26 \ rad + 2k \pi $$
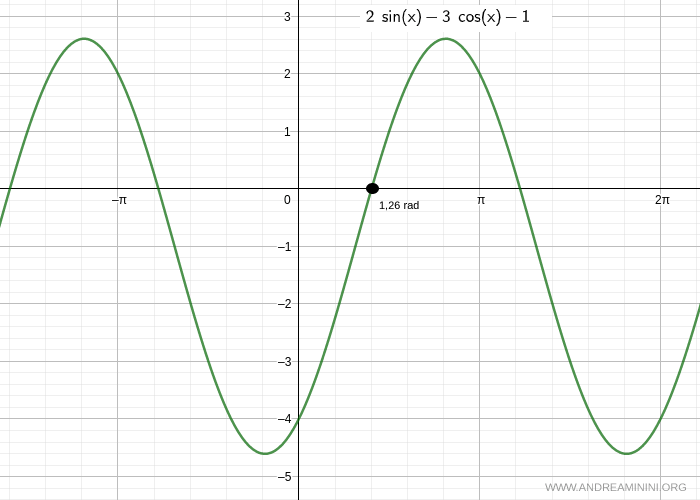
La seconda soluzione è la seguente equazione goniometrica elementare del tipo tan α = c
$$ \tan \frac{x}{2} = \frac{-2 - \sqrt{12}}{2} $$
Calcolo l'arcotangente a entrambi i membri
$$ \arctan ( \tan \frac{x}{2} ) = \arctan ( \frac{-2 - \sqrt{12}}{2} ) $$
$$ \frac{x}{2} = \arctan ( \frac{-2 - \sqrt{12}}{2} ) $$
A cui aggiungo kπ per includere anche le altre soluzioni con k intero
$$ \frac{x}{2} = \arctan ( \frac{-2 - \sqrt{12}}{2} ) + k \pi $$
L'arcotangente nel membro di destra è -1,22 radianti (-69,9°)
$$ \frac{x}{2} = -1,22 \ rad + k \pi $$
$$ x = - 2,44 \ rad + 2k \pi $$
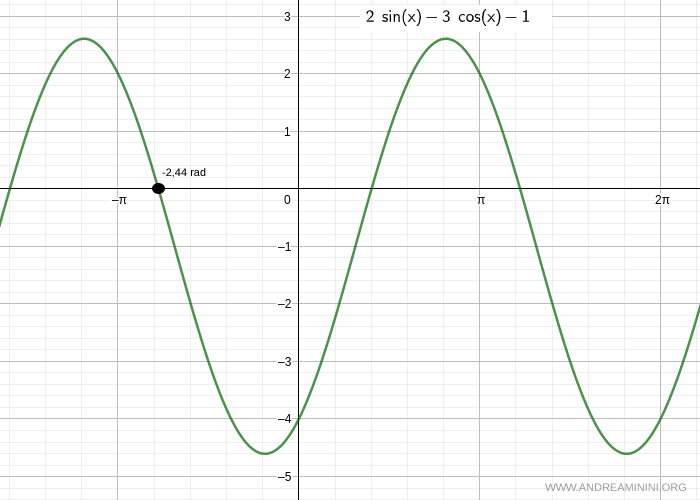
E così via.
