Angolo retto
Un angolo retto è un angolo che misura esattamente 90 gradi ossia pi greco mezzi radianti (π/2 rad).
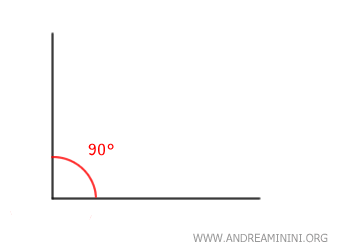
È uno degli angoli più fondamentali in geometria e viene spesso rappresentato con un piccolo quadrato nell'angolo.
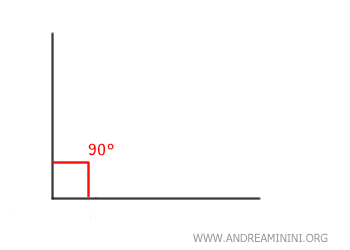
Un angolo retto si forma quando due linee si incontrano perpendicolarmente l'una all'altra.
L'angolo retto è la metà (1/2) di un angolo piatto (180°) e un quarto (1/4) di un angolo giro (360°).
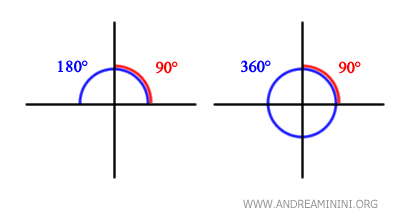
E' un concetto fondamentale in molti campi della matematica, della scienza e dell'ingegneria.
Ad esempio. In architettura e ingegneria, la perpendicolarità è fondamentale per la costruzione di edifici e strutture stabili. In matematica, gli angoli retti sono alla base di molte aree di studio, tra cui la trigonometria e la geometria euclidea. In fisica, gli angoli retti sono spesso utilizzati in problemi che coinvolgono vettori, dove la scomposizione di un vettore lungo assi perpendicolari può semplificare l'analisi.
Alcune osservazioni sugli angoli retti
L'angolo retto ha diverse proprietà uniche che lo rendono importante in molti campi della matematica e della fisica.
Ecco alcune delle proprietà più significative:
- Due rette perpendicolari formano quattro angoli retti.
Quando due linee si incrociano formando un angolo di 90 gradi, si dicono perpendicolari e creano quattro angoli retti.
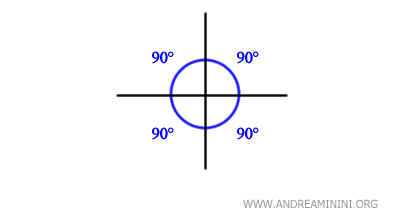
Questo è evidente nelle figure geometriche come il quadrato e il rettangolo, dove si possono sempre identificare quattro angoli di questo tipo.
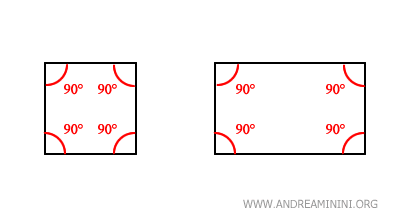
- Complementarità
Due angoli sono detti "angoli complementari" se la somma della loro ampiezza è un angolo retto.
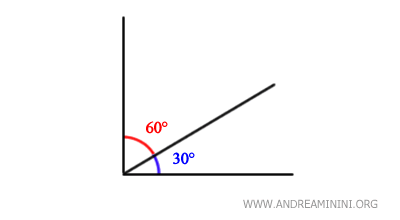
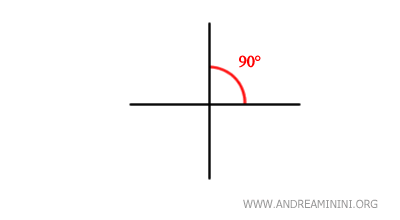
- Perpendicolarità
Due linee sono perpendicolari se formano un angolo retto tra di loro. Questa è una proprietà molto importante nella geometria euclidea.
- Triangolo rettangolo
In un triangolo rettangolo, l'angolo retto è l'angolo opposto al lato più lungo chiamato ipotenusa. - Teorema di Pitagora
Il teorema di Pitagora stabilisce che in un triangolo rettangolo, il quadrato della lunghezza dell'ipotenusa è uguale alla somma dei quadrati delle lunghezze degli altri due lati. Questa è una delle relazioni più fondamentali in tutta la matematica.
Storia
L'angolo retto è conosciuto fin dai tempi antichi.
Gli antichi egizi usavano delle corde annodate per creare un "triangolo egizio" di lati 3, 4 e 5, che è un tipico esempio di triangolo rettangolo, e lo usavano per realizzare angoli retti nelle costruzioni.
I numeri 3, 4 e 5 sono anche un esempio di "terna pitagorica"
Successivamente, gli antichi greci e in particolare Euclide svilupparono una geometria, detta geometria euclidea, in cui l'angolo retto gioca un ruolo centrale.
Ad esempio, il teorema di Pitagora è una delle più famose relazioni matematiche elaborate dagli antichi greci e riguarda specificamente i triangoli rettangoli, ossia i triangoli con un angolo retto.
E così via.
