L'equazione goniometrica sin(α)=-cos(α')

L'equazione goniometrica $$\sin \alpha = - \cos \alpha'$$ si risolve con la formula equivalente $$\sin \alpha = \sin (\alpha'-\frac{\pi}{2})$$ le cui soluzioni sono $$α = (\alpha'-\frac{\pi}{2}) + 2k \pi \ ∨ \ α+(\alpha'-\frac{\pi}{2}) = \pi + 2k \pi$$

Un esempio

Devo risolvere l'equazione goniometrica

$$\sin(\frac{1}{2}x) = -\cos(\frac{1}{4}x)$$

Trasformo la funzione coseno -cos(1/4x) in una funzione seno sin(1/4x-π/2)

$$\sin(\frac{1}{2}x) = \sin(\frac{1}{4}x- \frac{\pi}{2} )$$

In questo modo l'equazione diventa un'equazione del tipo sin α=sin α' dove.

$$\alpha = \frac{1}{2}x$$

$$\alpha' = \frac{1}{4}x - \frac{\pi}{2}$$

Applico la formula per trovare le soluzioni di un'equazione sin α=sin α'

$$α = α' + 2k \pi \ ∨ \ α+α' = \pi + 2k \pi$$

Dove k è un numero intero qualsiasi.

Sostituisco α e α'

$$\frac{1}{2}x = (\frac{1}{4}x - \frac{\pi}{2} ) + 2k \pi \ ∨ \ \frac{1}{2}x+(\frac{1}{4}x - \frac{\pi}{2} ) = \pi + 2k \pi$$

Svolgo i calcoli e metto in evidenza la x

$$\frac{1}{2}x - \frac{1}{4}x = - \frac{\pi}{2} + 2k \pi \ ∨ \ \frac{3}{4}x = \frac{\pi}{2} + \pi + 2k \pi$$

$$\frac{1}{4}x = - \frac{\pi}{2} + 2k \pi \ ∨ \ \frac{3}{4}x = \frac{3}{2} \pi + 2k \pi$$

$$x = 4 ( - \frac{\pi}{2} + 2k \pi ) \ ∨ \ +x = \frac{4}{3} \cdot ( \frac{3 }{2} \pi + 2k \pi )$$

$$x = - 2 \pi + 8k \pi \ ∨ \ +x = \frac{4}{3} \cdot \frac{3 }{2} \pi + \frac{4}{3} \cdot 2k \pi$$

$$x = - 2 \pi + 8k \pi \ ∨ \ +x = 2 \pi + \frac{8}{3} k \pi$$

In questo modo ottengo tutte le soluzioni dell'equazione sin x = sin y

A questo punto verifico se effettivamente le soluzioni soddisfano l'equazione goniometrica.

Verifico per k=0

$$x = - 2 \pi + 8k \pi \ ∨ \ +x = 2 \pi + \frac{8}{3} k \pi$$

$$x = - 2 \pi + 8(0) \pi \ ∨ \ +x = 2 \pi + \frac{8}{3} (0) \pi$$

$$x = - 2 \pi \ ∨ \ +x = 2 \pi$$

Pertanto una soluzione dell'equazione è x=-2π

Un'altra soluzione dell'equazione è x=2π

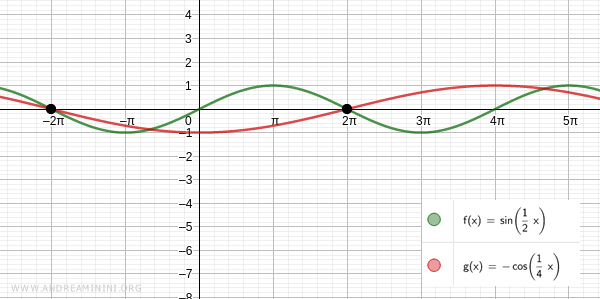
Verifico per k=1

$$x = - 2 \pi + 8k \pi \ ∨ \ +x = 2 \pi + \frac{8}{3} k \pi$$

$$x = - 2 \pi + 8(1) \pi \ ∨ \ +x = 2 \pi + \frac{8}{3} (1) \pi$$

$$x = 6 \pi \ ∨ \ +x = \frac{14}{3} \pi$$

Pertanto una soluzione dell'equazione è x=6π

Un'altra soluzione dell'equazione è x=14/3π

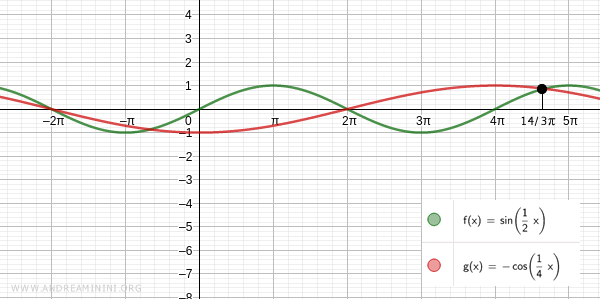
Verifico per k=-1

$$x = - 2 \pi + 8k \pi \ ∨ \ +x = 2 \pi + \frac{8}{3} k \pi$$

$$x = - 2 \pi + 8(-1) \pi \ ∨ \ +x = 2 \pi + \frac{8}{3} (-1) \pi$$

$$x = -10 \pi \ ∨ \ +x = - \frac{2}{3} \pi$$

Pertanto una soluzione dell'equazione è x=-10π

Un'altra soluzione dell'equazione è x=-2/3π

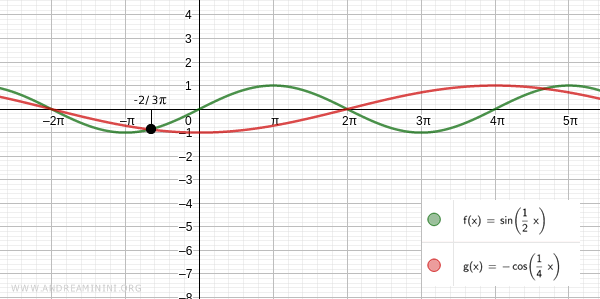
Variando la variabile k ottengo le altre infinite soluzioni dell'equazione goniometrica.

La dimostrazione

La funzione coseno

$$\cos \alpha$$

è strettamente legata alla funzione seno, perché il seno e il coseno sono sfasati di 90°(π/2) tra loro.

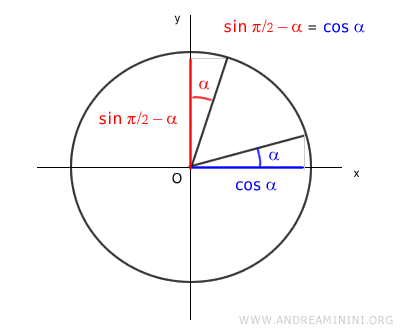
Quindi, posso riscrivere il coseno nella forma equivalente del seno usando un angolo associato (π/2-α)

$$\cos \alpha = \sin (\frac{\pi}{2} - \alpha )$$

Il seno e il coseno sono sfasati di 90° (πi/2) tra loro.

Pertanto, l'equazione goniometrica

$$\sin \alpha = - \cos \alpha'$$

posso riscriverla come

$$\sin \alpha = - \sin ( \frac{\pi}{2} - \alpha' )$$

Il seno è una funzione dispari -f(x)=f(-x)

Questo mi permette di cambiare il segno meno al secondo membro, portandolo nell'argomento.

$$\sin \alpha = \sin ( -\frac{\pi}{2} + \alpha' )$$

ossia

$$\sin \alpha = \sin (\alpha' -\frac{\pi}{2} )$$

In questo modo l'equazione diventa un'uguaglianza del tipo sin(α)=sin(β) le cui soluzioni sono

$$α = \beta + 2k \pi \ ∨ \ α+\beta = \pi + 2k \pi$$

In questo caso β = α'-π/2

$$α = ( \alpha'- \frac{\pi}{2} ) + 2k \pi \ ∨ \ α+( \alpha' - \frac{\pi}{2} ) = \pi + 2k \pi$$

Ho ottenuto la formula che volevo dimostrare.

E così via.