Angolo aggiunto in trigonometria

In trigonometria l'angolo aggiunto è un angolo che mi permette di scrivere una funzione $$y=a \sin x + b \cos x$$ in una funzione sinusoidale equivalente $$y = r \cdot \sin (x+k)$$

Dove k è l'angolo aggiunto ed è pari all'arcotangente del rapporto tra i coefficienti b/a.

$$k = \arctan \frac{b}{a}$$

Mentre r è l'ampiezza della sinusoide ed è la radice della somma dei quadrati dei coefficienti a²+b²

$$r = \sqrt{a^2+b^2}$$

Pertanto, una funzione sin(x)+cos(x) posso scriverla in una forma equivalente come una sinusoide tramite una traslazione orizzontale k e una dilatazione/contrazione verticale r.

$$y=a \sin x + b \cos x = r \cdot \sin (x+k)$$

Considerando le formule per ottenere r e k la formula di trasformazione completa è la seguente

$$y=a \sin x + b \cos x = \sqrt{a^2+b^2} \cdot \sin (x+\arctan \frac{b}{a})$$

Attenzione. Nella formula di trasformazione devo usare gli stessi segni dei coefficienti a e b nella funzione iniziale. Ad esempio, se la funzione iniziale è $$y= \sin x - \cos x$$ I coefficienti a e b sono $$a=1$$ $$b=-1$$

Un esempio pratico

Prendo in considerazione questa funzione dove a=2 e b=3

$$y=2 \sin x - 3 \cos x$$

Il grafico della funzione è il seguente

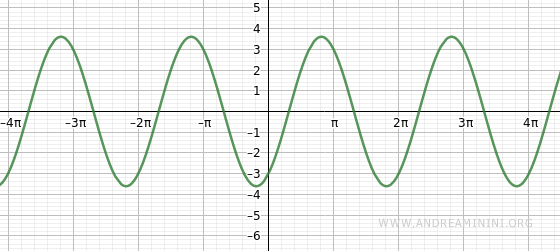
Devo trasformarla nella forma equivalente

$$y = r \sin (x+k)$$

L'angolo aggiunto k è l'arcotangente del rapporto b/a

$$k = \arctan \frac{b}{a} = \arctan \frac{-3}{2} = - 0,98 \ rad \ (circa \ -56,3°)$$

L'ampiezza r è la radice quadrata della somma dei quadrati a²+b²

$$r = \sqrt{a^2+b^2} = \sqrt{2^2+3^2} = \sqrt{4+9} = \sqrt{13}$$

Pertanto nella forma equivalente la funzione è

$$y = \sqrt{13} \cdot \sin (x + (-0,98 \ rad ))$$

$$y = \sqrt{13} \cdot \sin (x - 0,98 \ rad)$$

Si ottiene con una dilatazione di √13 e una traslazione di -0,98 radianti (circa -56,3°).

Il grafico della funzione sinusoidale appena ottenuta è uguale al grafico iniziale.

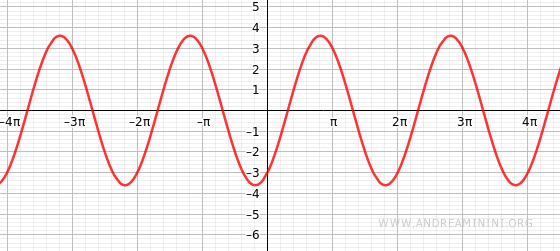
La dimostrazione

La formula che voglio dimostrare è una funzione sinusoidale

$$y = r \sin (x+k)$$

Applico la formula dell'addizione del seno.

$$y = r \cdot [ \sin x \cos k + \sin k \cos x ]$$

$$y = r \sin x \cos k + r \sin k \cos x$$

Assegno i due addendi alle variabili a e b

$$a = r \cos k$$

$$b = r \sin k$$

In questo modo ho scritto la funzione nella forma equivalente

$$y = a \sin x + b \cos x$$

Per avere questa forma equivalente i coefficienti a e b devono soddisfare questo sistema

$$\begin{cases} a = r \cos k \\ \\ b = r \sin k \end{cases}$$

Elevo al quadrato i membri delle equazioni

$$\begin{cases} a^2 = r^2 \cos^2 k \\ \\ b^2 = r^2 \sin^2 k \end{cases}$$

Sommo le due equazioni membro a membro

$$a^2 + b^2 = r^2 \cos^2 k + r^2 \sin^2 k$$

$$a^2 + b^2 = r^2 ( \cos^2 k + \sin^2 k )$$

Secondo la prima relazione fondamentale della trigonometria la somma del coseno quadro e del seno quadro è uguale a uno ossia cos²+sin²=1

Quindi semplifico l'equazione

$$a^2 + b^2 = r^2$$

A questo punto applico la radice quadrata a entrambi i membri dell'equazione

$$\sqrt{a^2 + b^2} = \sqrt{r^2}$$

$$\sqrt{a^2 + b^2} = r$$

Ho così trovato il valore del coefficiente r ossia l'ampiezza della sinusoide.

Per trovare l'angolo k torno al sistema di equazioni.

$$\begin{cases} a = r \cos k \\ \\ b = r \sin k \end{cases}$$

Poi divido membro a mebro le due equazioni

$$\frac{b}{a} = \frac{r \sin k}{r \cos k}$$

$$\frac{b}{a} = \frac{\sin k}{\cos k}$$

$$\frac{b}{a} = \tan k$$

Applico l'arcotangente a entrambi i membri dell'equazione

$$\arctan \frac{b}{a} = \arctan \tan k$$

$$\arctan \frac{b}{a} = k$$

Ho così trovato anche l'angolo aggiunto k della sinusoide.

$$k = \arctan \frac{b}{a}$$

E così via.