Teorema della base nella topologia di sottospazio
Dato uno spazio topologico \(X\) con una base \( B_X \) , cioè una collezione di insiemi aperti che "genera" la topologia su \(X\) , e un sottoinsieme \(Y\) di \(X\), allora la collezione di intersezioni degli elementi di \( B_X \) con \(Y\) forma una base \( B_Y \) per la topologia sottospazio su \(Y\). $$ B_Y = \{ B \cap Y \ | \ B \in B_X \} $$
Esempio
Vediamo di rendere tutto questo un po' più concreto con un esempio semplice.
Considero lo spazio topologico \( \mathbb{R} \) con la topologia standard che ha come base l'insieme degli intervalli aperti \((a, b)\), dove \( a < b \).
Ora, prendo il sottoinsieme \(Y = [0, 2]\) di \( \mathbb{R} \).
Voglio trovare una base per la topologia sottospazio su \(Y\).
La base per la topologia standard sull'insieme dei numeri reali \( \mathbb{R} \) è :
$$ B_{\mathbb{R}} = \{(a, b) \ | \ a, b \in \mathbb{R}, \ a < b \} $$
Nota. In altre parole la base dei numeri reali è una collezione di insiemi (a,b) con a<b dove a,b sono numeri reali. Ogni insieme aperto in può essere espresso come un'unione di tali intervalli aperti. Ad esempio, l'insieme aperto (0,3) posso ottenerlo unendo gli insiemi aperti (0,2)U(1,3), l'insieme aperto (2,5) posso ottenerlo tramite l'unione degli insiemi aperti (2,4)U(3,6) ecc.
La base per la topologia del sottospazio $ Y $ è l'intersezione tra tutti gli insiemi aperti (a.b) della base in $ \mathbb{R} $ e l'insieme $ Y = [0,2] $ del sottospazio topologico.
$$ B_Y = \{ (a, b) \cap [0, 2] \ | \ (a, b) \in B_{\mathbb{R}} \} $$
Ecco alcuni elementi che possono far parte di \( B_Y \):
Ad esempio, prendo l'insieme aperto \( (a, b) = (-1, 1) \) nella topologia in $ \mathbb{R} $
$$ (-1, 1) \cap [0, 2] = [0, 1) $$
Quindi, \([0, 1) \) è un elemento che appartiene alla base \( B_Y \).
Prendo \( (a, b) = (1, 3) \) nella topologia in $ \mathbb{R} $
$$ (1, 3) \cap [0, 2] = (1, 2] $$
Quindi, \( (1, 2] \) è un altro elemento della base \( B_Y \).
Prendo \( (a, b) = (0.5, 1.5) \) nella topologia in $ \mathbb{R} $
$$ (0.5, 1.5) \cap [0, 2] = (0.5, 1.5) $$
Quindi, anche \( (0.5, 1.5) \) è un elemento di \( B_Y \). E via dicendo.
A questo punto verifico la base \( B_Y \):
Considero un insieme aperto \(W\) nella topologia sottospazio su \(Y\), ad esempio \(W = (0.5, 1.5]\).
L'insieme \(W = (0.5, 1.5] \) è aperto in \(Y\) perché esiste un insieme aperto \(U\) in \( \mathbb{R} \) tale che \(W = U \cap [0, 2]\). Ad esempio \(U = (0.5, 1.5]\).
$$ W = U \cap [0, 2] = (0.5, 1.5] \cap [0, 2] = (0.5,1.5] $$
Considero un punto \(y \in W\), ad esempio \( y = 1 \).
Siccome \(U = (0.5, 1.5]\) è aperto in \( \mathbb{R} \), esiste un elemento base \( (a, b) \in B_{\mathbb{R}} \) tale che \( y \in (a, b) \subseteq U \).
In questo caso, posso prendere \( (a, b) = (0.8, 1.2) \).
Intersecando \( (a, b) \) con \( [0, 2] \) ottengo:
$$ (0.8, 1.2) \cap [0, 2] = (0.8, 1.2) $$
Quindi, \( (0.8, 1.2) \) è un elemento di \( B_Y \) che contiene \( y = 1 \) e sta in \( W = (0.5, 1.5] \).
Questo conferma che ogni punto di \( W \) è coperto da un elemento di \( B_Y \) e dimostra che \( B_Y \) è una base per la topologia sottospazio su \(Y\).
Dimostrazione
Nella topologia in $ X $ considero un sottoinsieme $ X \subset Y $
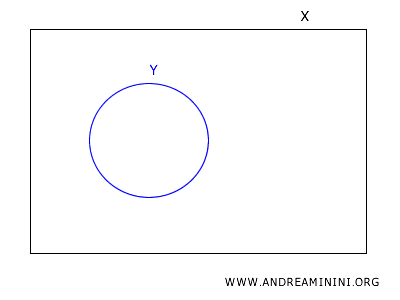
La base \(B_Y\) è la collezione di insiemi formati intersecando ogni elemento della base \(B_X\) con il sottoinsieme \(Y\).
Ogni elemento di \(B_Y\) è un insieme aperto nella topologia sottospazio su \(Y\).
Devo dimostrare che \(B_Y\) è una base per la topologia sottospazio su \(Y\).
Considero un insieme aperto \(W\) nella topologia sottospazio su \(Y\).
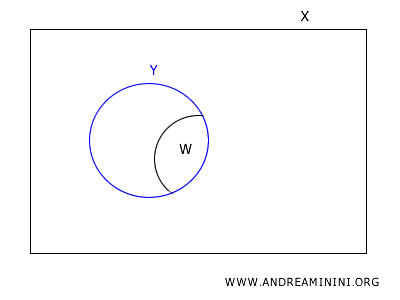
Poiché \(W\) è aperto in \(Y\), esiste un insieme aperto \(U\) in \(X\) tale che \(W = U \cap Y\).
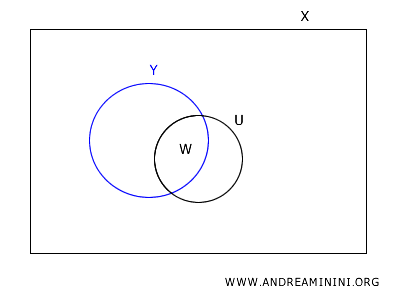
Prendo un punto arbitrario \(y\) in \(W\).
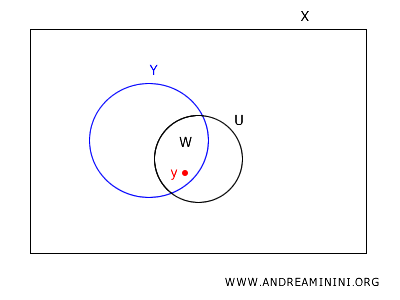
Siccome \(U\) è aperto in \(X\), per la definizione di base, esiste un elemento base \(B \in B_X\) tale che \(y \in B \subseteq U\).
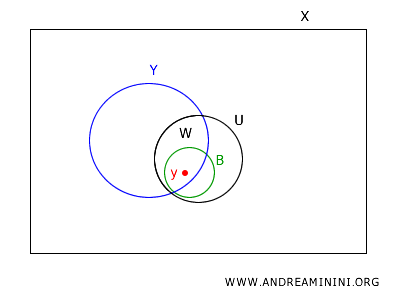
Intersecando \(B\) con \(Y\), ottengo \(B \cap Y \in B_Y\), che contiene \(y\) e sta in \(W\). Quindi, ogni punto di \(W\) è coperto da un elemento di \(B_Y\).
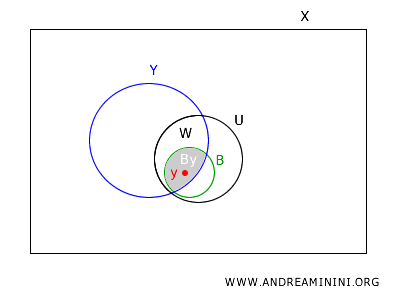
In conclusione, ogni punto \(y\) in \(W\) è contenuto in un elemento di \(B_Y\) che è contenuto in \(W\).
$$ y \in B_Y = B \cap Y \subseteq U \cap Y = W $$
Questo dimostra che \(B_Y\) è una base per la topologia sottospazio su \(Y\).
E così via.
