Grafi
Cos'è un grafo
Un grafo G=(V,E) è una struttura relazionale composta da un insieme dei vertici o vertex V={1, 2, …, n) e un insieme di coppie di vertici (i,j) detti spigoli o edges E={ e1, e2, … , em }.
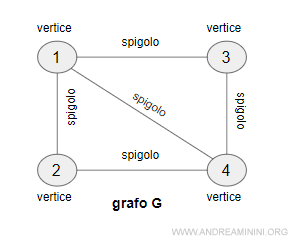
Per rappresentare il grafo indico i vertici con dei cerchi. All'interno di ogni cerchio scrivo l'etichetta identificativa del vertice. Può essere un numero o una lettera.
I vertici di un grafo G formano un insieme di elementi:
$$ V(G) = \{ 1,2,3,4 \} $$
Gli spigoli o lati, invece, sono le linee che collegano i vincoli. Possono essere orientati o non orientati. Gli spigoli orientati hanno un verso di percorrenza e sono anche detti archi.
$$ E(G) = \{ (1,2),(1,3), (1,4), (2,4),(3,4) \} $$
Nota. I termini "vertici" e "spigoli" (o lati) usati in un grafo dervano dalla geometria solida. Ad esempio, un cubo ha otto vertici e 12 spigoli.
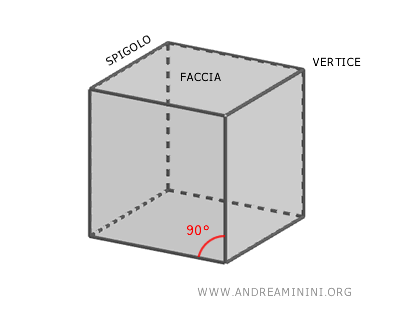
Lo stesso cubo posso immaginarlo anche come un insieme di vertici e di lati di un grafo.
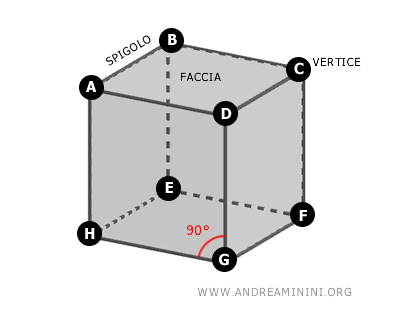
Volendo posso anche modificare nella forma del grafo senza causare alcuna perdita di significato. Questo perché nella teoria dei grafi la forma specifica o la disposizione spaziale degli oggetti è meno importante delle relazioni tra gli oggetti.
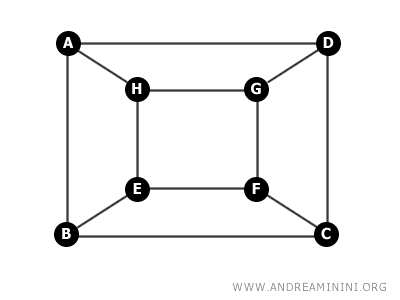
Nel caso degli spigoli è preferibile parlare di "famiglia" di lati piuttosto che insieme di lati, perché in un grafo possono esserci anche lati multipli, ossia due o più spigoli, tra due vertici. In un insieme, invece, non può esserci lo stesso elemento ripetuto più volte.
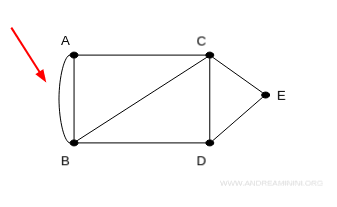
Ad esempio, in questo grafo ci sono due lati (spigoli) tra i vertici A e C.
A cosa serve un grafo? I grafi hanno diverse applicazioni pratiche. Sono utilizzati per modellare le reti di computer, le relazioni sociali, le mappe stradali, le reti di trasporto, i circuiti elettrici, e molto altro. Ad esempio, in informatica, i grafi sono alla base degli algoritmi di ricerca come quelli per trovare il percorso più breve in una rete stradale o per analizzare le reti sociali. In generale i grafi offrono un linguaggio universale per la descrizione di strutture e processi complessi.
Un esempio pratico
Questo grafo è composto da 4 vertici e 5 spigoli.

L'insieme dei vertici V del grafo G è composto da quattro vertici.
$$ V(G) = { 1,2,3,4 } $$
L'insieme degli spigoli E del grafo G è composto da cinque spigoli
$$ E(G) = { (1.2),(1,3),(1,4),(2.4),(3,4) } $$
Ogni spigolo (linea) è una coppia ordinata di vertici detti estremi.
Il primo elemento indica il vertice di partenza, il secondo elemento il vertice di destinazione.
Nota. Non essendoci un verso, ogni spigolo permette lo spostamento in entrambe le direzioni. Pertanto, lo spigolo (a,b) è uguale allo spigolo (b,a). Ad esempio, gli spigoli (1,2) e (2,1) sono lo stesso spigolo. E via dicendo.
Esempio 2
In alternativa posso rappresentare il grafo anche in questa forma più sintetica.
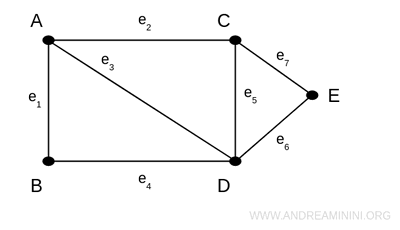
In questa rappresentazione i vertici (vertices) sono dei punti e gli spigoli (edges) sono linee.
Ogni vertice è etichettato con una lettera maiuscola.
Esempio 3
Questo grafo è composto da 5 vertici e 8 spigoli.
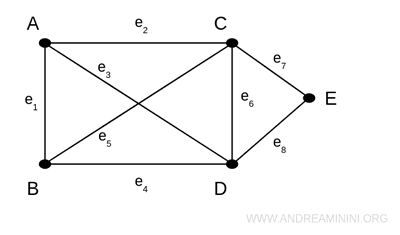
L'intersezione dello spigolo (A,D) e (B,C) non è un vertice perché non c'è alcun punto (vertice).
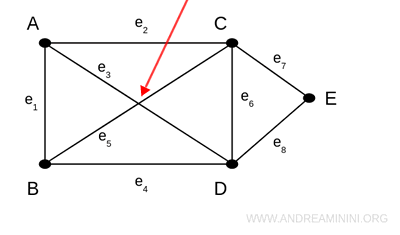
Questo vuol dire che i due spigoli (A,D) e (B,C) non sono collegati tra loro. Non sono un "incrocio".
Lo spigolo (A,D) passa sopra (o sotto) l'altro spigolo (B,C) come un cavalcavia sull'autostrada.
A volte per indicare meglio questa situazione si mette un ponticello in uno dei due spigoli.
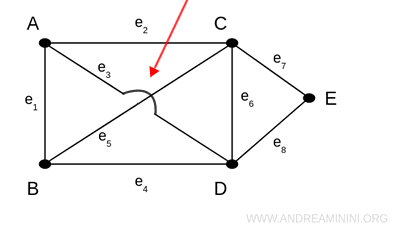
Nota. Per rappresentare questa situazione posso anche collegare il vertice senza intersezioni. Tuttavia, questa rappresentazione non è facile da costruire quando gli spigoli sono molti. Inoltre, si perde il concetto visivo di lunghezza dello spigolo.
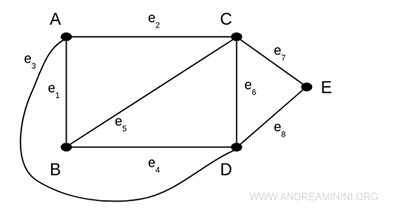
La disposizione dei vertici del grafo è comunque indifferente.
Ad esempio, potrei riscrivere il grafo precedente anche in questa forma equivalente:
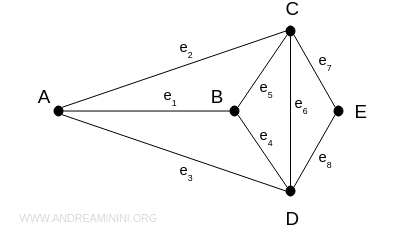
Vertici e lati adiacenti in un grafo
In un grafo due vertici sono vertici adiacenti se c'è un lato che li collega.
Ad esempio, i vertici A e B sono adiacenti perché sono collegati tra loro tramite il lato e1.

Allo stesso modo, due lati (spigoli o archi) sono lati adiacenti se hanno un vertice in comune.
Ad esempio, i lati e1 e e2 sono lati adiacenti perché sono entrambi lati del vertice A.
Le diverse notazioni per indicare i lati
Per rappresentare i lati (spigoli, archi) di un grafo posso usare diverse notazioni.
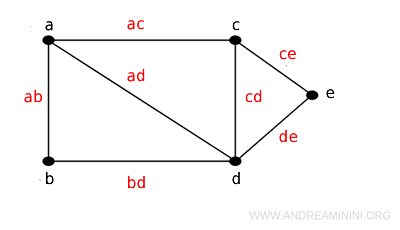
Ad esempio, posso indicare i lati del grafo come una coppia ordinata di vertici: (a,b), (a,c), ecc.
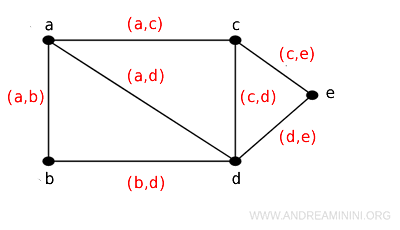
Tuttavia, spesso per brevità è consuetudine indicare i lati come ab, bc, ecc.
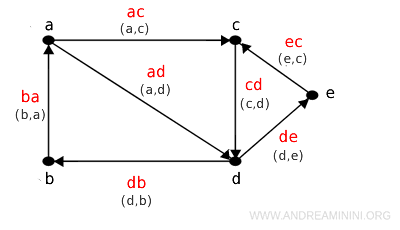
Nota. Nel caso dei grafi orientati (digrafi) la prima lettera indica il nodo di origine mentre la seconda lettera il nodo di destinazione. Questo vale per entrambe le notazioni.
Le caratteristiche dei grafi
I grafi hanno diverse caratteristiche che li contraddistingono, ne elenco le principali.
- Ordine di un grafo
E' il numero di vertici nel grafo. - Dimensione di un grafo
E' il numero di archi nel grafo. - Grado di un vertice
E' il numero di archi o spigoli che incidono su un vertice. Nei grafi orientati (digrafi), si distingue tra il grado in entrata (numero degli archi in entrata su un vertice) e il grado in uscita (numero degli archi in uscita da un vertice). - Percorso
Un percorso è una sequenza di vertici in cui ciascun vertice è adiacente al successivo. - Ciclo
Un ciclo è un percorso chiuso in cui l'unico vertice ripetuto è quello di inizio/fine. - Connettività
Un grafo si dice connesso se esiste un percorso tra ogni coppia di vertici.
Il grado di un vertice
Il grado di un vertice indica il numero di spigoli collegati al vertice stesso.
Ad esempio, il vertice A è di grado 3 perché ha tre spigoli.
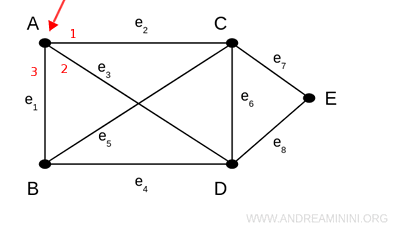
Il vertice E è di grado 2 perché ha due spigoli.
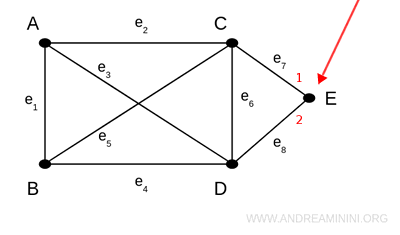
Nota. Questi esempi sono detti grafi semplici perché non contengono spigoli multipli o loop.
Quando si calcola il grado di un vertice, i cappi devono essere devono essere contati due volte.
I cappi sono dei lati (spigoli o archi) che collegano lo stesso vertice.
Ad esempio, in questo grafo il vertice A ha grado 4 perché ha due lati spigoli incidenti e un cappio che vale per due.
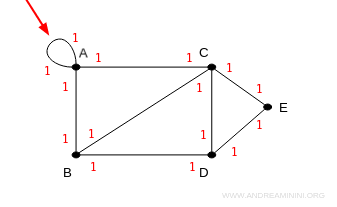
Una volta calcolati i gradi di tutti gli spigoli, spesso è utile scrivere la sequenza dei gradi scritti in ordine crescente.
Ad esempio, questi sono i gradi di tutti i vertici del grafo.
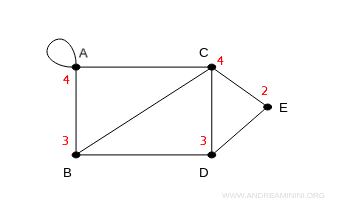
Partendo dal grado più basso (2), la sequenza dei nodi è la seguente
$$ \{ 2 , 3, 3, 4, 4 \} $$
Lemma della stretta di mano. In ogni grafo la somma dei gradi dei vertici è un numero pari. Questo è dovuto al fatto che ogni lato è collegato a due vertici. Quindi, la somma dei gradi dei vertici del grafo è uguale al doppio del numero dei lati del grafo. Essendo il "doppio" è un numero "pari", perché il prodotto di qualsiasi numero per un numero pari è a sua volta un numero pari.
Gli spigoli multipli
Gli spigoli multipli (multiple edges) sono spigoli che hanno in comune gli stessi vertici agli estremi.
Ad esempio, due spigoli collegano i vertici A e B

Questi due spigoli sono spigoli multipli.
I loop
Un loop (o cappio) è uno spigolo che collega lo stesso vertice.
Ad esempio, in questo grafo il vertice A ha un loop.
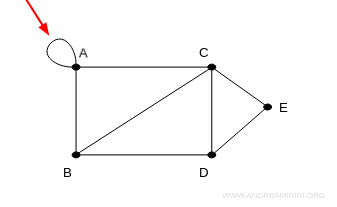
Lo spigolo ha lo stesso vertice (A) in entrambi gli estremi.
Il cammino sul grafo può procedere all'infinito restando sullo stesso vertice.
Tipologie di grafi
Esistono diversi tipi di grafi:
- Grafi non orientati
Sono grafi in cui gli spigoli non hanno una direzione. Ci si può muovere in entrambi i versi tra gli estremi di ogni spigolo. - Grafi orientati (digrafi)
In questi grafi gli spigoli hanno verso di percorrenza. Gli spigoli sono anche detti "archi" mentre i vertici sono detti "nodi". - Grafi semplici
Sono grafi senza cappi (loop) e senza lati multipli. - Grafi pesati
In un grafo pesato ogni arco/spigolo ha un peso o costo associato. - Grafi non pesati
Gli spigoli/archi non hanno pesi associati. - Grafi ciclici e aciclici
Un grafo è ciclico se contiene almeno un ciclo, altrimenti è detto aciclico. - Alberi
Gli alberi sono un caso speciale di grafo aciclico e connesso.
I digrafi
I digrafi (digraphs o directed graphs) sono grafi direzionali in cui gli spigoli hanno un verso di percorrenza.
Ad esempio, questo grafo è un digrafo.
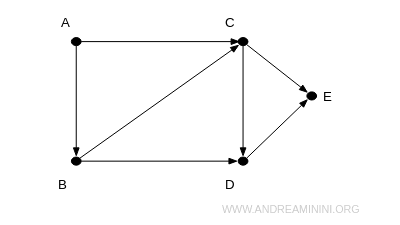
Il grafo consente lo spostamento dal vertice A al vertice B ma non il contrario.
Nel caso dei digrafi gli spigoli direzionali (directed edges) sono anche detti archi (arc) e mentre i vertici sono detti nodi.
La differenza tra cammini, percorsi e cicli
In un grafo un cammino (walk) è una sequenza di vertici connessi da spigoli o archi.
Ad esempio, la sequenza A→B→C→D→E→C è un cammino di lunghezza 5.
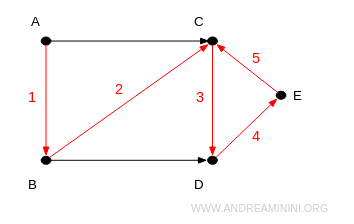
Un percorso (path) è una sequenza di vertici connessi tra loro spigoli o archi in cui nessun vertice appare più di una volta.
Ad esempio, la sequenza A→B→C→D→E→C è un percorso di lunghezza 4.
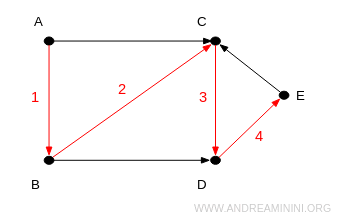
Il ciclo (cycle) è un cammino in cui il vertice iniziale e finale della sequenza sono lo stesso vertice e nessun altro vertice della sequenza appare più di una volta.
Ad esempio, la sequenza A→B→C→A è un ciclo.
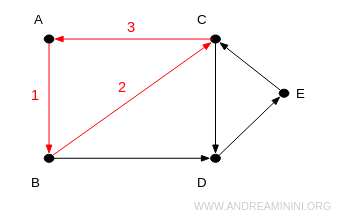
E così via.
