Risolvere un equazione lineare in seno e coseno con l'angolo aggiunto

Un'equazione lineare in seno e coseno $$ a \sin x + b \cos x + c = 0 $$ si può trasformare tramite l'angolo aggiunto in un'equazione elementare $$ r \sin(x+k)+ c $$ la cui soluzione è $$ \sin(x+k) = - \frac{c}{r} $$

Dove r è l'ampiezza della sinusoide

$$ r = \sqrt{a^2+b^2} $$

mentre il parametro k è l'angolo aggiunto

$$ k = \arctan \frac{b}{a} $$

Nota sui segni. Quanto detto funziona bene se $ a $ e $ b $ sono positivi. Tuttavia, in caso contrario, è importante fare attenzione ai segni relativi del seno e del coseno. Se uno o entrambi i coefficienti $ a $ e $ b $ sono negativi, bisogna determinare in quale quadrante si trova l’angolo aggiunto $ k $ per evitare errori nel risultato finale. La tangente dell’angolo aggiunto rimane la stessa, ma l'angolo stesso potrebbe trovarsi in un quadrante diverso. Quindi, potrebbe essere necessario adattare l'angolo a seconda dei segni di $ a $ e $ b $.

A cosa serve?

Un'equazione goniometrica elementare si risolve molto più facilmente di un'equazione lineare in seno e coseno.

Un esempio pratico

Devo risolvere l'equazione lineare in seno e coseno

$$ \sqrt{3} \sin x + \cos x = \sqrt{3} $$

ossia

$$ \sqrt{3} \sin x + \cos x - \sqrt{3} = 0 $$

Applico il metodo dell'angolo aggiunto

$$ r \sin (x +k) + c = 0 $$

$$ \sqrt{a^2+b^2} \sin (x +k) + c = 0 $$

Sapendo che a=√3 , b = 1 , c=-√3

$$ \sqrt{(\sqrt{3})^2+1^2} \sin (x + k) - \sqrt{3} = 0 $$

$$ \sqrt{3+1} \sin (x + k) - \sqrt{3} = 0 $$

$$ \sqrt{4} \sin (x + k) - \sqrt{3} = 0 $$

$$ 2 \sin (x + k) - \sqrt{3} = 0 $$

L'angolo aggiunto k=arctan(b/a) ossia k=arctan(1/√3)

$$ 2 \sin (x + \arctan(\frac{1}{\sqrt{3}})) - \sqrt{3} = 0 $$

Sposto i termini noti a destra

$$ \sin (x + \arctan(\frac{1}{\sqrt{3}})) = \frac{\sqrt{3}}{2} $$

Moltiplico e divido per √3

$$ \sin (x + \arctan(\frac{1}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} ) ) = \frac{\sqrt{3}}{2} $$

$$ \sin (x + \arctan(\frac{\sqrt{3}}{3} ) ) = \frac{\sqrt{3}}{2} $$

La tangente assume il valore √3/3 con un angolo π/6 radianti (ossia 30°)

Quindi l'arcotangente di √3/3 è π/6

$$ \sin (x + \frac{\pi}{6} ) = \frac{\sqrt{3}}{2} $$

Questa è un'equazione goniometrica elementare sin(α)=numero che ammette infinite soluzioni

$$ x + \frac{\pi}{6} = \alpha + 2\pi k \vee x + \frac{\pi}{6} = (\pi - \alpha) + 2\pi k $$

Dove k è un numero intero qualsiasi.

Resta da capire qual è l'angolo α.

Considerando α = x+π/6 il seno sin(α)=√3/2 quando α = π/3 radianti (ossia 60°)

$$ x + \frac{\pi}{6} = \frac{\pi}{3} + 2\pi k \vee x + \frac{\pi}{6} = (\pi - \frac{\pi}{3}) + 2\pi k $$

$$ x = \frac{\pi}{3} - \frac{\pi}{6} + 2\pi k \vee x = \pi - \frac{\pi}{3} - \frac{\pi}{6} + 2\pi k $$

$$ x = \frac{2 \pi - \pi}{6} + 2\pi k \vee x = \frac{6 \pi - 2 \pi - \pi}{6} + 2\pi k $$

$$ x = \frac{\pi}{6} + 2\pi k \vee x = \frac{3 \pi}{6} + 2\pi k $$

$$ x = \frac{\pi}{6} + 2\pi k \vee x = \frac{\pi}{2} + 2\pi k $$

Quando k=0 l'equazione ha due soluzioni x=π/6 e x=π/2

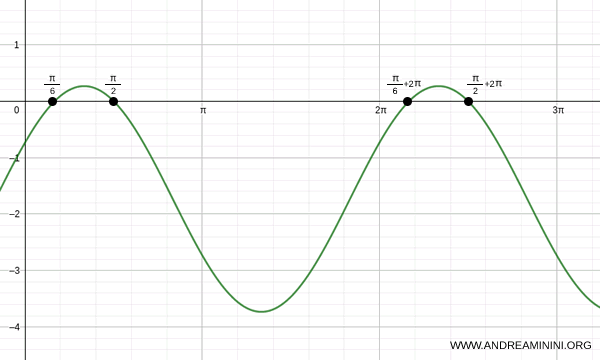
Variando k trovo tutte le altre soluzioni periodiche dell'equazione lineare in seno e coseno.

Esempio 2

Considero l’equazione lineare in seno e coseno

$$ -\sqrt{3} \sin x + \cos x = \sqrt{3}, $$

che riscrivo come

$$ -\sqrt{3} \sin x + \cos x - \sqrt{3} = 0. $$

In questo caso, i coefficienti sono \( a = -\sqrt{3} \), \( b = 1 \), e \( c = -\sqrt{3} \).

Sottolineo che il coefficiente $ a < 0 $ è negativo, vediamo cosa cambia nella risoluzione dell'equazione.

Applico il metodo dell'angolo aggiunto:

$$ r \sin (x + k) + c = 0, $$

Dove \( r = \sqrt{a^2 + b^2} \) e \( k = \arctan\left(\frac{b}{a}\right) \).

Calcolo \( r \):

$$ r = \sqrt{(-\sqrt{3})^2 + 1^2} = \sqrt{3 + 1} = \sqrt{4} = 2 $$

Ora, calcolo l'angolo aggiunto \( k \):

$$ k = \arctan\left(\frac{1}{-\sqrt{3}}\right). $$

La tangente di \( k \) è \( -\frac{1}{\sqrt{3}} \), che corrisponde a un angolo di \( -\frac{\pi}{6} \) (o \( 330^\circ \)) nel quarto quadrante dove il coseno è positivo e il seno è negativo.

Tuttavia, poiché \( a < 0 \) e \( b > 0 \), l’angolo \( k \) deve trovarsi nel secondo quadrante dove il seno è positivo e il coseno è negativo, rispettando i segni di \( a \) e \( b \).

Per posizionare correttamente \( k \) nel secondo quadrante, aggiungo \( \pi \) a \( -\frac{\pi}{6} \):

$$ k = -\frac{\pi}{6} + \pi = \frac{5\pi}{6}. $$

Nota. Se non correggessi \( k \) aggiungendo \( \pi \), otterrei un angolo nel quadrante sbagliato, che porta a un risultato errato. Usare \( k = -\frac{\pi}{6} \) (quarto quadrante) invece di \( k = \frac{5\pi}{6} \) (secondo quadrante) porterebbe quindi a una soluzione basata su una funzione sinusoidale che non rispecchia correttamente i segni di \( a \) e \( b \). Questo errore genererebbe un’equazione diversa da quella di partenza, quindi con soluzioni che non risolvono correttamente l’equazione originale.

A questo punto, una volta adattato l'angolo al quadrante giusto, sostituisco l'angolo \( k = \frac{5\pi}{6} \) nell'equazione:

$$ 2 \sin\left(x + \frac{5\pi}{6}\right) - \sqrt{3} = 0. $$

Sposto i termini noti a destra:

$$ \sin\left(x + \frac{5\pi}{6}\right) = \frac{\sqrt{3}}{2} $$

Questa è un'equazione goniometrica elementare del tipo \( \sin(\alpha) = \text{numero} \), che ammette infinite soluzioni:

$$ x + \frac{5\pi}{6} = \alpha + 2\pi k \quad \text{oppure} \quad x + \frac{5\pi}{6} = (\pi - \alpha) + 2\pi k $$

Dove \( k \) è un numero intero qualsiasi.

Ora, calcolo l’angolo \( \alpha \). Poiché \( \sin(\alpha) = \frac{\sqrt{3}}{2} \), trovo che \( \alpha = \frac{\pi}{3} \). Sostituendo nelle soluzioni:

$$ x + \frac{5\pi}{6} = \frac{\pi}{3} + 2\pi k \quad \text{oppure} \quad x + \frac{5\pi}{6} = \pi - \frac{\pi}{3} + 2\pi k $$

Da qui otteniamo le soluzioni:

$$ x = \frac{\pi}{3} - \frac{5\pi}{6} + 2\pi k = -\frac{\pi}{2} + 2\pi k $$

$$ x = \pi - \frac{\pi}{3} - \frac{5\pi}{6} + 2\pi k = \frac{\pi}{6} + 2\pi k $$

Quindi le soluzioni finali dell’equazione sono:

$$ x = -\frac{\pi}{2} + 2\pi k \quad \text{e} \quad x = \frac{\pi}{6} + 2\pi k $$

Ecco le prime due soluzioni sul grafico per k=0 e k=1.

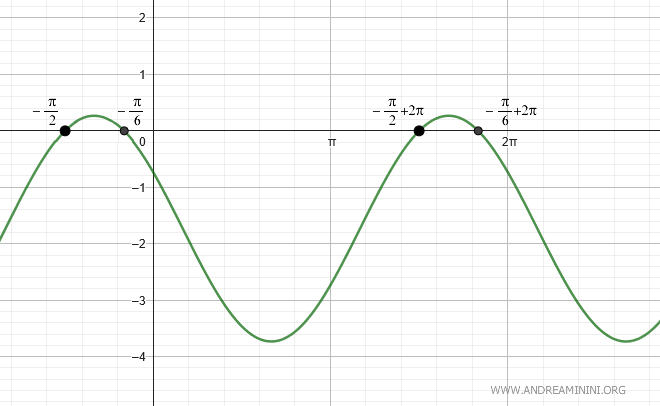
Questo esempio mostra l'importanza di considerare i segni di \( a \) e \( b \) e di adattare il valore di \( k \) per collocarlo nel quadrante corretto, ottenendo così il risultato corretto.

La dimostrazione

L'angolo aggiunto è un angolo che permette di trasformare un'equazione goniometrica lineare in seno e coseno

$$ y = a \sin x + b \cos x $$

in un'equazione sinusoidale equivalente

$$ y = r \cdot sin (x+k) $$

Dove r è l'ampiezza della sinusoide

$$ r = \sqrt{a^2+b^2} $$

mentre k è l'angolo aggiunto pari all'arcotangente del rapporto dei coefficienti b/a

$$ k = \arctan \frac{b}{a} $$

Pertanto, un'equazione lineare in seno e coseno

$$ a \sin x + b \cos x + c = 0 $$

posso riscriverla nella forma equivalente

$$ r \sin (x+k) + c = 0 $$

Sposto i termini noti c e r a destra

$$ \sin (x+k) = - \frac{c}{r} $$

Questa equazione è un'equazione goniometrica elementare del tipo sin(alfa)=numero

Quindi, si può risolvere abbastanza facilmente.

E così via.