L'equazione goniometrica del tipo cot a = cot b

L'equazione goniometrica $$ \cot \alpha = \cot \alpha' $$ si risolve con gli angoli associati trasformando la cotangente in una tangente $$ \tan (\frac{\pi}{2} - \alpha) = \tan (\frac{\pi}{2} - \alpha') $$ usando la stessa risoluzione delle equazioni tan x=tan y. $$ (\frac{\pi}{2} - \alpha) = (\frac{\pi}{2} - \alpha') +k \pi $$

Un esempio pratico

Devo risolvere l'equazione goniometrica

$$ \cot \frac{1}{2} x + \frac{\pi}{2} = \cot \frac{5}{2} x - \frac{\pi}{2}$$

Trasformo la cotangente in tangente in entrambi i membri dell'equazione

$$ \tan ( \frac{\pi}{2} - \frac{1}{2} x + \frac{\pi}{2} ) = \tan ( \frac{\pi}{2} - \frac{5}{2} x - \frac{\pi}{2}) $$

Gli angoli delle tangenti sono

$$ \alpha = \frac{\pi}{2} - \frac{1}{2} x + \frac{\pi}{2}$$

$$ \alpha' = \frac{\pi}{2} - \frac{5}{2} x - \frac{\pi}{2} $$

Applico la regola di risoluzione delle equazioni tan α = tan α' per trovare le soluzioni dell'incognita x.

$$ \alpha = \alpha' +k \pi $$

In questo caso α=π/2-1/2x+1/2π e α'=π/2-5/2x-1/2π

$$ \frac{\pi}{2} - \frac{1}{2} x + \frac{\pi}{2} = \frac{\pi}{2} - \frac{5}{2} x +k \pi - \frac{\pi}{2}$$

Svolgo i calcoli e metto in evidenza l'incognita x

$$ \frac{5}{2} x - \frac{1}{2} x = \frac{\pi}{2} - \frac{\pi}{2} +k \pi - \frac{\pi}{2} - \frac{\pi}{2} $$

$$ \frac{4}{2} x = k \pi -\pi $$

$$ 2 x = k \pi - \pi $$

$$ x = \frac{1}{2} ( k \pi - \pi) $$

$$ x = \frac{1}{2} k \pi - \frac{1}{2} \pi) $$

Ora per trovare le soluzioni mi basta variare la variabile intera k.

Verifico per k=0

$$ x = \frac{1}{2} k \pi - \frac{1}{2} \pi) $$

$$ x = \frac{1}{2} (0) \pi - \frac{1}{2} \pi) $$

$$ x = - \frac{1}{2} \pi) $$

La prima soluzione dell'equazione goniometrica è x=-1/2π

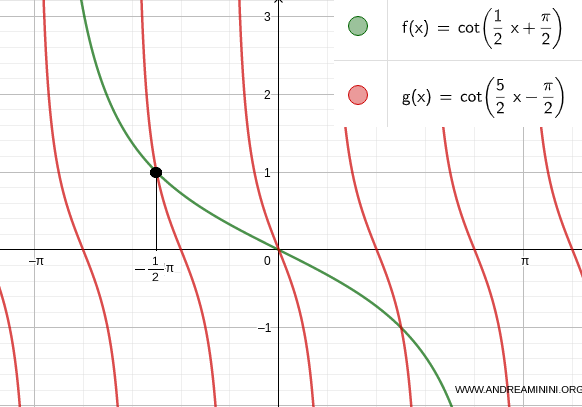
Verifico per k=1

$$ x = \frac{1}{2} k \pi - \frac{1}{2} \pi) $$

$$ x = \frac{1}{2} (1) \pi - \frac{1}{2} \pi) $$

$$ x = \frac{1}{2} \pi - \frac{1}{2} \pi) $$

$$ x = 0 $$

La seconda soluzione dell'equazione goniometrica è la soluzione banale x=0

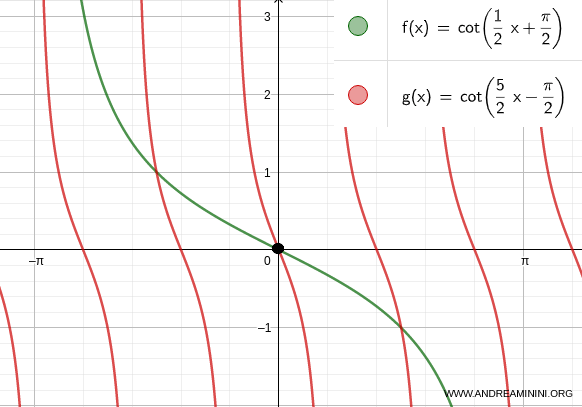
Verifico per k=2

$$ x = \frac{1}{2} k \pi - \frac{1}{2} \pi) $$

$$ x = \frac{1}{2} (2) \pi - \frac{1}{2} \pi) $$

$$ x = \pi - \frac{1}{2} \pi) $$

$$ x = \frac{1}{2} \pi) $$

La terza soluzione dell'equazione goniometrica è x=1/2π

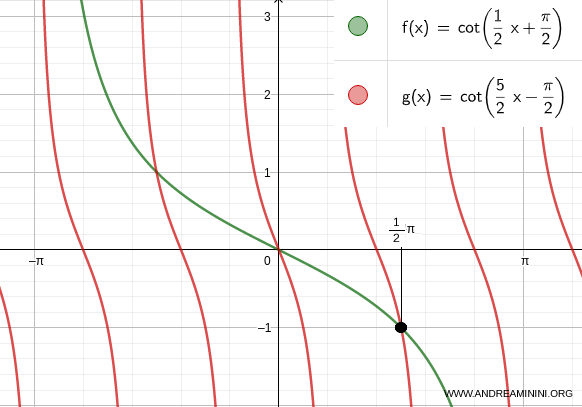
Variando k=2,-2, 3, -3, ... trovo le altre infinite soluzioni dell'equazione goniometrica.

La dimostrazione

Tra la tangente e la cotangente c'è una relazione inversa

$$ \cot \alpha = \frac{1}{ \tan \alpha} $$

Pertanto, la cotangente è nulla quando la tangente tende a più o meno infinito e viceversa.

Gli angoli associati alfa (α) e π/2-α mi permettono di trasformare la cotangente in una tangente

$$ \cot \alpha = \tan (\frac{\pi}{2} - \alpha) $$

Pertanto, l'equazione goniometrica

$$ \cot \alpha = \cot \alpha' $$

Posso riscriverla in forma equivalente usando la funzione tangente dell'angolo associato π/2-α

$$ \tan (\frac{\pi}{2} - \alpha) = \tan (\frac{\pi}{2} - \alpha') $$

In questo modo l'equazione cot α = cot α' diventa un'equazione goniometrica tan x = tan y la cui risoluzione è la seguente.

$$ x = y +k \pi $$

Dove k è un numero intero qualsiasi moltiplicato per π rad perché la tangente e la cotangente sono funzioni periodiche con periodo π radianti (180°).

In questo caso gli argomenti della tangente sono x=π/2-α e y=π/2-α'

$$ \tan (\frac{\pi}{2} - \alpha) = \tan (\frac{\pi}{2} - \alpha') +k \pi $$

Questo dimostra la formula di risoluzione dell'equazione goniometrica cot α = cot α'.

E così via.