L'equazione della bisettrice di un angolo
La bisettrice di un angolo è la semiretta che ha origine dal vertice dell'angolo dividendo l'ampiezza in due angoli congruenti. L'equazione della bisettrice è la seguente: $$ \frac{ax+by+c}{ \sqrt{a^2+b^2}} = \pm \frac{a'x+b'y+c'}{ \sqrt{a'^2+b'^2}} $$
Questa equazione rappresenta le due bisettrici che dividono un angolo in due angoli congruenti.
Il segno ± indica che esistono due bisettrici: una che divide l'angolo acuto e una l'angolo ottuso formati dall'intersezione delle due rette.
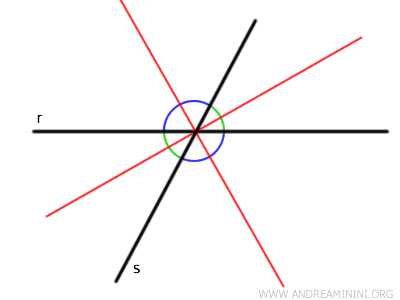
Nota. Questa formula deriva dal fatto che i punti sulla bisettrice sono equidistanti dalle due rette. La bisettrice è il luogo geometrico dei punti che hanno uguale distanza dalle due rette.
Un esempio pratico
Considero le equazioni di due rette non parallele tra loro.
$$ r : 3x+4y-6=0 $$
$$ s: 4x-3y-4=0 $$
Le due rette sono incidenti e formano due coppie di angoli congruenti, una coppia di angoli acuti e una coppia di angoli ottusi.
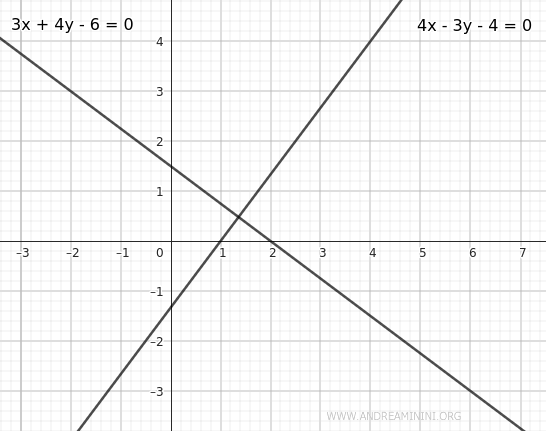
Per trovare l'equazione delle due bisettrici utilizzo la formula seguente:
$$ \frac{ax+by+c}{ \sqrt{a^2+b^2}} = \pm \frac{a'x+b'y+c'}{ \sqrt{a'^2+b'^2}} $$
Sostituisco i coefficienti delle due rette r e s ovvero a=3, b=4, c=-6 e a'=4, b'=-3, c'=-4.
$$ \frac{3x+4y-6}{ \sqrt{3^2+4^2}} = \pm \frac{4x-3y-4}{ \sqrt{4^2+(-3)^2}} $$
$$ \frac{3x+4y-6}{ \sqrt{9+16}} = \pm \frac{4x-3y-4'}{ \sqrt{16+9}} $$
$$ \frac{3x+4y-6}{ \sqrt{25}} = \pm \frac{4x-3y-4}{ \sqrt{25}} $$
$$ \frac{3x+4y-6}{ 5 } = \pm \frac{4x-3y-4}{ 5} $$
Per la proprietà invariantiva delle equazioni, moltiplico entrambi i lati per 5 e semplifico.
$$ \frac{3x+4y-6}{ 5 } \cdot 5 = \pm \frac{4x-3y-4}{ 5} \cdot 5 $$
$$ 3x+4y-6 = \pm (4x-3y-4) $$
A questo punto considero i singoli casi, quello in cui il segno nel secondo membro dell'equazione è più oppure meno.
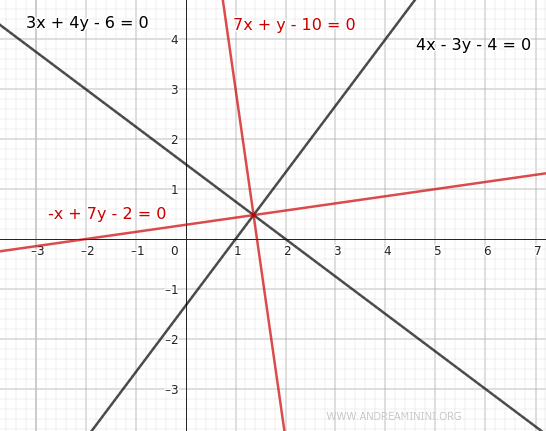
- Caso 1 (+) $$ 3x+4y-6 = + (4x-3y-4) $$ $$ 3x+4y-6 - 4x + 3y+4 = 0 $$ In questo modo trovo l'equazione di una bisettrice $$ -x+7y-2 = 0 $$
- Caso 2 (-) $$ 3x+4y-6 = - (4x-3y-4) $$$$ 3x+4y-6 = -4x+3y+4) $$ $$ 3x+4y-6 + 4x - 3y-4 = 0 $$ In questo modo trovo l'equazione dell'altra bisettrice $$ 7x+y-10 = 0 $$
Ho così trovato entrambe le equazioni delle bisettrici delle due coppie di angoli opposti.
La dimostrazione
Un angolo è compreso tra due semirette r e s dette "lati" dell'angolo, che hanno origine da un punto detto "vertice" dell'angolo.
Considero le equazioni delle due rette:
$$ r: \ ax+by+c=0 $$
$$ s: \ a'x+b'y+c'=0 $$
La bisettrice è una semiretta che ha origine dal vertice dell'angolo e ha la caratteristica di avere ogni punto equidistante dai lati dell'angolo.
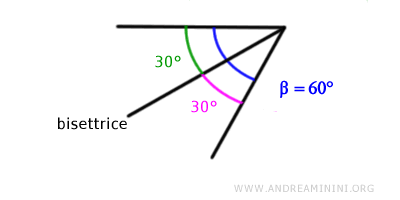
Quindi, la bisettrice è il luogo dei punti equidistanti dai lati dell'angolo.
Ad esempio, se considero il punto P sulla bisettrice, la distanza di P dalla retta r è il segmento $ \overline{AP} $ perpendicolare a r che ha come estremo P e un punto A della retta r. Allo stesso modo la distanza da P dalla retta s è il segmento $ \overline{BP} $.
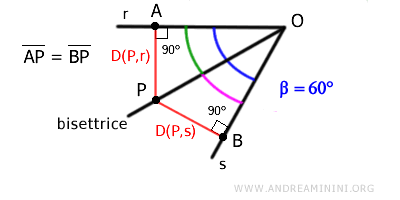
Il punto P è equidistante da entrambe le rette solo se i segmenti AP≅BP sono congruenti, ovvero se i segmenti AP e BP hanno la stessa distanza.
$$ \overline{AP} \cong \overline{BP} $$
Pertanto, i punti che hanno la stessa distanza soddisfano l'equazione:
$$ D(P,r) = D(P,s) $$
La formula che misura la distanza D(P,r) di un punto P(x;y) dalla retta r è la seguente:
$$ D(P,r) = \frac{|ax+by+c|}{ \sqrt{a^2+b^2}} $$
Quella che misura la distanza D(P,s) dalla retta s è invece la seguente:
$$ D(P,s) =\frac{|a'x+b'y+c'|}{ \sqrt{a'^2+b'^2}} $$
Nota. È importante ricordare che le distanze sono espresse in valore assoluto perché la distanza è una lunghezza di un segmento e deve essere sempre un valore non negativo.
Sostituisco le formule delle distanze D(P,r) e D(P,s) nell'uguaglianza.
$$ D(P,r)=D(P,s) $$
$$ \frac{|ax+by+c|}{ \sqrt{a^2+b^2}} = \frac{|a'x+b'y+c'|}{ \sqrt{a'^2+b'^2}} $$
Tuttavia, il ragionamento non è ancora concluso, perché quando due rette si intersecano tra loro formano quattro angoli, ovvero due coppie di angoli opposti e congruenti.

Quindi le bisettrici da considerare sono due rette perpendicolari tra loro. Una bisettrice divide l'angolo acuto mentre l'altra divide l'angolo ottuso.
Per trovare entrambe le equazioni delle bisettrici, tolgo il modulo al primo membro dell'equazione e considero entrambi i segni possibili nel secondo membro.
$$ \frac{ax+by+c}{ \sqrt{a^2+b^2}} = \pm \frac{a'x+b'y+c'}{ \sqrt{a'^2+b'^2}} $$
Questo dimostra la formula dell'equazione della bisettrice degli angoli formati da due rette.
E così via.
