Come calcolare l'area di un settore circolare

Posso calcolare l'area di un settore circolare conoscendo il raggio (r) della circonferenza e la lunghezza dell'arco (l) $$ Area_{settore} = \frac{l \cdot r}{2} $$ oppure l'angolo in radianti (α) e il quadrato del raggio (r²) $$ Area_{settore} = \frac{\alpha \cdot r^2}{2} $$

Esempio pratico

Prendo in considerazione una circonferenza con raggio r=3 e un settore circolare con un angolo di α=28,44°.

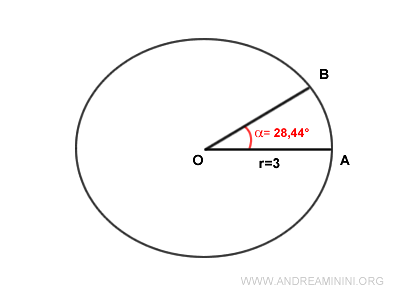
Per prima cosa trasformo l'angolo in radianti.

$$ \alpha = 28,44° \cdot \frac{ \pi }{180°} = 0,5 \ rad $$

Attenzione. E' molto importante usare l'angolo in radianti. Lascare l'angolo in gradi è un errore grave che invalida tutti i calcoli.

Una volta ottenuto l'angolo in radianti posso calcolare facilmente la lunghezza dell'arco AB del settore circolare

$$ AB = \alpha \cdot r $$

$$ AB = 0,5 \ rad \ \cdot 3 =1,5 \ $$

Quindi, la lunghezza dell'arco è l=1,5

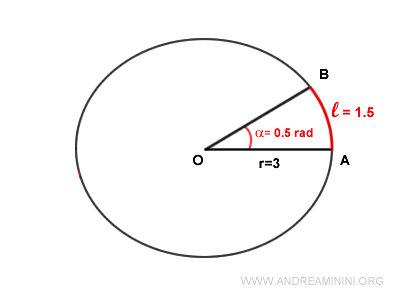
Nota la lunghezza dell'arco (l=1,5) e del raggio (r=3) calcolo l'area del settore circolare

$$ A_{s} = \frac{l \cdot r}{2} $$

$$ A_{s} = \frac{1,5 \cdot 3}{2} = 2,25 $$

L'area del settore circolare è 2,25.

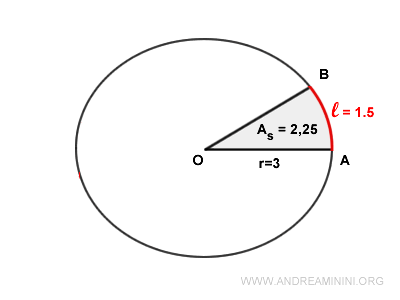
Nota. Allo stesso risultato sarei potuto arrivare usando la seconda formula una volta noto l'angolo in radianti e il raggio. $$ A_{s} = \frac{\alpha \cdot r^2}{2} = \frac{ 0,5 \ \cdot 3^2 }{2} = \frac{ 4,5 }{2} = 2,25 $$

La dimostrazione

La formula dell'area di un settore circolare si dimostra facendo una proporzione.

L'area del settore circolare sta all'area del cerchio come l'angolo sta all'angolo giro in radianti (2p).

$$ Area_{settore} \ : \ Area_{cerchio} = \alpha \ : \ 2 \pi $$

ossia

$$ \frac{ Area_{settore} }{ Area_{cerchio} } = \frac{ \alpha } { 2 \pi } $$

Metto in evidenza l'area del settore

$$ Area_{settore} = \frac{ \alpha } { 2 \pi } \cdot Area_{cerchio} $$

Sapendo che l'area del cerchio π·r²

$$ Area_{settore} = \frac{ \alpha } { 2 \pi } \cdot \pi r^2 $$

Semplifico pi greco (π) e ottengo la seconda formula.

$$ Area_{settore} = \frac{ \alpha } { 2 } \cdot r^2 $$

Riscrivo l'angolo come rapporto tra la lunghezza dell'arco e il raggio (l/r)

$$ Area_{settore} = \frac{ 1 } { 2 } \cdot \frac{ l }{ r } \cdot r^2 $$

Semplifico il raggio (r)

$$ Area_{settore} = \frac{ 1 } { 2 } \cdot l \cdot r $$

In questo modo ottengo anche la prima formula

$$ Area_{settore} = \frac{ l \cdot r } { 2 } $$

Ho dimostrato le due formule.

E così via.