Come calcolare l'angolo tra due rette
Due rette r e r’ che si intersecano in un punto del piano $$ y=m \cdot x + q \\ y’ = m' \cdot x’ + q' $$ formano un angolo gamma pari all'arcotangente del rapporto $$ \gamma = \arctan \frac{m-m'}{1+m \cdot m'} $$
Dove m e m’ sono i coefficienti angolari delle rette.
Un esempio pratico
Prendo in considerazione due rette
$$ r: \ \ \ y = 4x-3 $$
$$ r': \ \ \ y = -x+3 $$
Calcolo l'angolo tra le due rette incidenti usando la formula.
$$ \gamma = \arctan \frac{m-m'}{1+m \cdot m'} $$
Il coefficiente angolare della prima retta è m=4 mentre quello della seconda retta è m'=-1
$$ \gamma = \arctan \frac{4-(-1)}{1+4 \cdot (-1)} $$
$$ \gamma = \arctan \frac{5}{-3} $$
$$ \gamma = -59,03° $$
$$ \gamma =59,03° $$
Dal punto di vista grafico
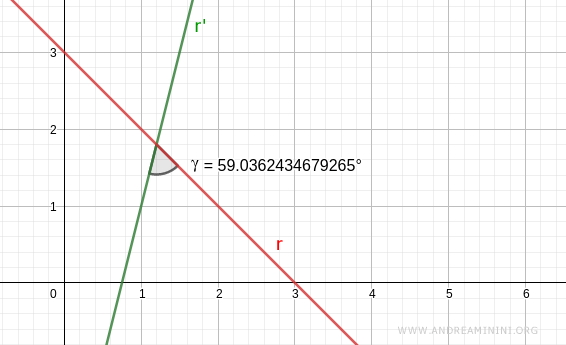
L'altro angolo tra le rette è un angolo supplementare.
Quindi, si calcola per differenza tra 180° (π rad) e l'angolo γ.
$$ γ' = π - γ $$
$$ γ' = 180° - 59,03° $$
$$ γ' = 120,96° $$
Dal punto di vista grafico.
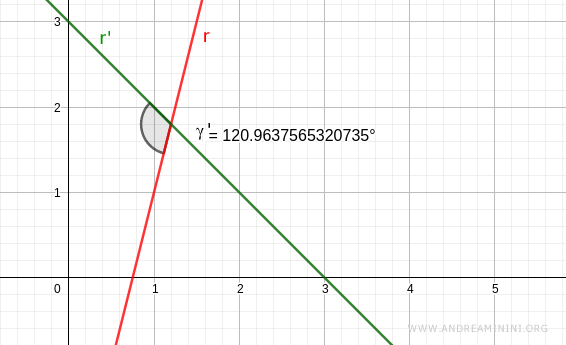
Nota. Gli altri due angoli dell'intersezione sono angoli opposti. Pertanto, sono uguali a quelli appena calcolati.
Esempio 2
Ho due rette incidenti r e r'
$$ r: \ \ \ y = 3x-2 $$
$$ r': \ \ \ y = x+4 $$
Calcolo l'angolo tra le due rette incidenti con la formula.
$$ \gamma = \arctan \frac{m-m'}{1+m \cdot m'} $$
Il coefficiente angolare della prima retta è m=3 mentre quello della seconda retta è m'=1
$$ \gamma = \arctan \frac{3-(1)}{1+3 \cdot 1} $$
$$ \gamma = \arctan \frac{2}{4} $$
$$ \gamma = \arctan \frac{1}{2} $$
$$ \gamma = 26,56° $$
Dal punto di vista grafico.
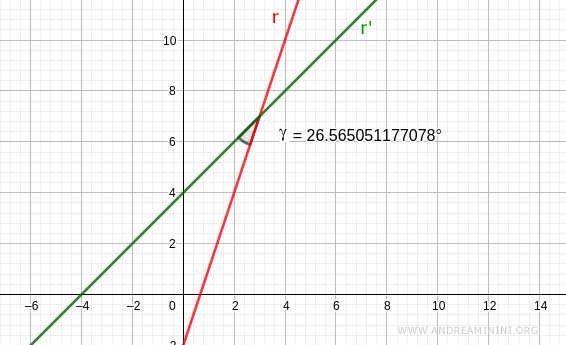
L'altro angolo tra le rette è un angolo supplementare.
Quindi, si calcola per differenza tra 180° (π rad) e l'angolo γ.
$$ γ' = π - γ $$
$$ γ' = 180° - 26,53° $$
$$ γ' = 153,43° $$
Dal punto di visto grafico
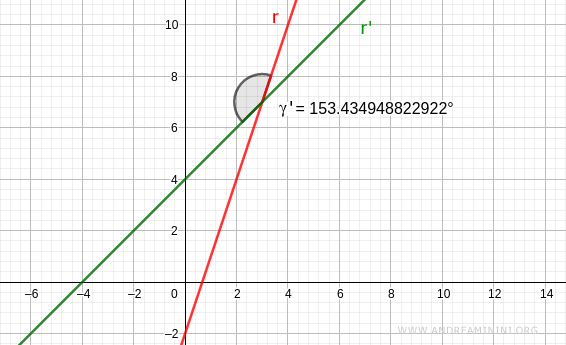
Nota. Gli altri due angoli dell'intersezione sono angoli opposti. Pertanto, sono uguali a quelli appena calcolati.
La dimostrazione
Per calcolare l'angolo tra due rette è d'aiuto la trigonometria.
Due rette incidenti (non parallele) r e r’ si intersecano in un punto P del piano.
$$ r: \ \ y=m \cdot x + q $$ $$ r’ : \ \ y’ = m' \cdot x’ + q' $$
Dove m e m' sono i coefficienti angolari delle rette.
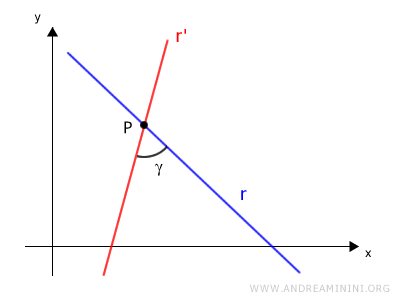
Le due rette intersecano in due punti sull'asse dell'ascisse A e B formando due angoli α e β con l'asse.
$$ \alpha = \tan \frac{y}{x} = m $$
$$ \beta = \tan \frac{y'}{x'} = m' $$
L'unione dei punti A, B, P con tre segmenti forma un triangolo ABP.
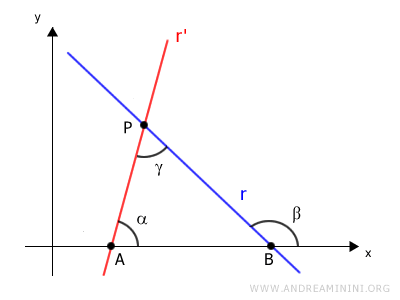
La somma degli angoli interni di un triangolo è π radianti (180°).
L'angolo beta (β) è un angolo esterno al triangolo ed è uguale alla somma degli angoli interni non adiacenti beta (β) e gamma (γ) perché è un angolo supplementare all'angolo interno β'.
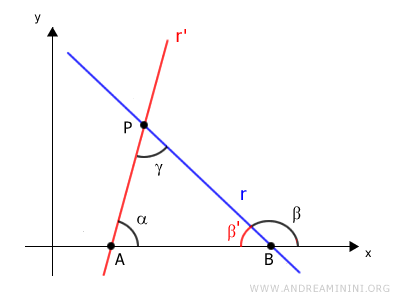
Pertanto, posso scrivere l'equazione
$$ \beta = \alpha + \gamma $$
Metto in evidenza l'angolo gamma
$$ \gamma = \beta - \alpha $$
Calcolo la tangente a entrambi i membri dell'equazione
$$ \tan \gamma = \tan ( \beta - \alpha ) $$
Poi applico la formula della sottrazione della tangente al secondo membro dell'equazione.
$$ \tan \gamma = \frac{\tan \beta - \tan \alpha }{1 + \tan \beta \cdot \tan \alpha } $$
Sapendo che la tangente dell'angolo alfa è uguale al coefficiente angolare m della prima retta tan α = m
$$ \tan \gamma = \frac{\tan \beta - m }{1 + \tan \beta \cdot m } $$
e che la tangente dell'angolo beta è uguale al coefficiente angolare m' della seconda retta tan β = m'
$$ \tan \gamma = \frac{m' - m}{1 + m' \cdot m} $$
Se il valore della tangente è positivo si tratta dell'angolo acuto tra le due rette. Viceversa, se la tangente è negativa si tratta dell'angolo ottuso tra le due rette.
Calcolo l'arcotangente a entrambi i membri dell'equazione e ottengo l'angolo gamma (γ) ossia l'angolo tra le due rette.
$$ \arctan \tan \gamma = \arctan \frac{m' - m}{1 + m' \cdot m} $$
$$ \gamma = \arctan \frac{m' - m}{1 + m' \cdot m} $$
Ho ottenuto la formula che volevo dimostrare.
Nota. In questa dimostrazione il coefficiente m' compare prima di m, al minuendo della sottrazione, semplicemente perché in questo caso il lato dell'angolo comincia con la retta r' in senso antiorario. E' solo una questione di nome delle variabili. La sostanza non cambia.

E così via.
